二分搜尋樹的原理與Java源碼實現

1 折半查詢法

瞭解二叉查詢樹之前，先來看看折半查詢法,也叫二分查詢法 在一個有序的整數陣列中（假如是從小到大排序的），如果查詢某個元素，返回元素的索引。

如下：

思想很簡單: 1 先找到陣列中間元素target與6比較 2 如果target比6大，就在陣列的左邊查詢 3 如果target比6小，就在陣列的右邊查詢

java實現程式碼如下：

測試程式碼如下：

2.4 二叉搜尋樹的刪除

二叉搜尋樹最麻煩的就是刪除節點，刪除任意二叉樹中的節點之前，我們來先刪除特殊的節點。

1. 刪除二叉搜尋樹中最小的節點

2. 刪除二叉搜尋樹中最大的節點

3. 查詢二叉搜尋樹中最小的節點

4. 查詢二叉搜尋樹中最大的節點

我們先來實現這些操作。

如下圖

根據二叉搜尋樹的定義，可以得出以下結論

1. 在一個二叉搜尋樹中，最小的節點一定是最左邊的節點，也就是圖中的節點 3

2. 在一個二叉搜尋樹中，最大的節點一定是最右邊的節點，也就是圖中的節點 18

總之： 最小節點去左子樹中找，直到節點的左孩子為空，則當前節點就是最小節點 最大節點去右子樹中找，直到節點的右孩子為空，則當前節點就是最大節點

1 先來實現查詢二叉搜尋樹中最小的節點 如下程式碼

同理，查詢最大節點也是一樣 2 實現查詢二叉搜尋樹中最大的節點 程式碼如下：

上面實現了查詢最小節點和最大節點，下面我們再來實現刪除最小節點和刪除最大節點

3 實現刪除二叉搜尋樹中最小的節點 一直往左孩子中刪除，當某一個節點node沒有左孩子時，說明當前節點就是最小節點 這時候分兩種情況

1. 當前節點有右孩子 如果是這種情況，直接把右孩子返回，作為當前節點

2. 當前節點沒有右孩子 如果是這種情況，直接返回null。此時返回右孩子也行，因為右孩子也是null

程式碼實現如下

同理，刪除二叉搜尋樹中最大的節點的程式碼如下：

下面來分析一下刪除任意一個節點。 刪除任意一個節點node，那麼可以分為以下幾種情況

1. node 沒有孩子

2. node 只有一個孩子

3. node 有兩個孩子

如下圖一棵二叉搜尋樹，我們來分析

第一種情況：node沒有孩子 這種情況最簡單，直接刪除就行了，剩下的還是一棵二叉搜尋樹 比如圖中的 節點5，節點13，節點27，節點50，刪除任意一個節點之後 剩下的還是滿足一棵二叉搜尋樹

第二種情況：node只有一個孩子 這種情況又分兩種

1. node節點有一個左孩子

2. node節點有一個右孩子

上面兩種情況其實不影響，比如圖中的節點10，節點45,分別有一個左孩子和一個右孩子。 也好辦，節點10刪除後，它的左孩子節點5，放在節點10的位置 同理知，節點45刪除後，它的右孩子節點50，放在節點45的位置 這樣一來，剩下的節點還是一棵二叉搜尋樹

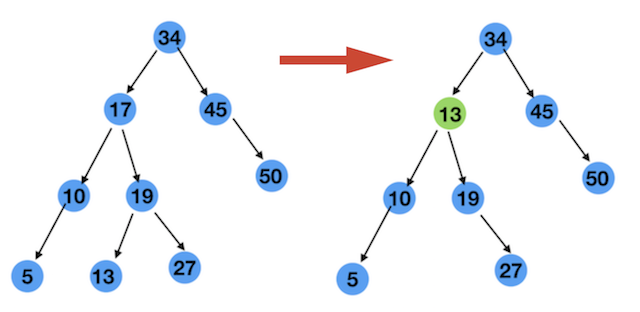
第三種情況：node有兩個孩子 還是上圖為準，以節點17為例，節點17有左右兩個孩子,分別是10，19 要刪除節點17，怎麼辦呢？ 或者說節點17刪除 後，哪個節點應該放在節點17的位置上呢？

我們節點17滿足兩個性質 ：

1. 17大於它的左孩子10

2. 17小於它的右孩子19

那麼我們找到一個這樣的節點，只要滿足上面這兩條性質，不就是可以了嗎。 so easey

我們就來先找一個大於10而且小於19的節點

1. 大於 10 的節點，只要在 17 的右子樹 也就是以 19 為根節點的樹中找不就行了嗎 因為17的右子樹中所有的節點都比 17 大

2. 小於 19 的節點，只要在以 19 為根的樹中找左孩子不就得了嗎 經過上面的分析，這樣的節點就是 13 啊，將17刪除 ，把13放到17的位置 ，如圖

其實，把10放到17的位置也是可以的。如下圖

10和13兩個節點都滿足條件，所以我們可以得出結論

刪除一個有兩個孩子節點，可以找這個節點左子樹中的最大節點，或者右子樹中的最小節點來放到當前位置

s 可以叫做 d 的後繼 s.right = deledeMin(d->right) s.left = d.left; 刪除 d, s 是新的子樹的根

翻譯成程式碼如下：

同過上面的分析，我們瞭解了二叉搜尋樹的性質，以及插入，查詢，查詢最大節點，查詢最小節點，刪除最大節點，刪除最小節點，以及最後分析出來刪除一個任意節點。

下面我們粘出完整程式碼 。如下

想了解更多精彩內容，快來關注計算機java程式設計