來源：資料STUDIO

作者：Jim

之前我們學習了一般線性迴歸，以及加入正則化的嶺迴歸與Lasso，其中嶺迴歸可以處理資料中的多重共線性，從而保證線性迴歸模型不受多重共線性資料影響。Lasso主要用於高維資料的特徵選擇，即降維處理。

線性迴歸中的多重共線性與嶺迴歸

深度理解Lasso迴歸分析

在使用線性迴歸時，除了遇到以上問題（資料中存在多重共線性、資料維度過高），還會遇到資料並不總是線性的，若此時仍堅持用線性模型去擬合非線性資料，其結果往往是很糟糕的。慶幸地是除了更換更加複雜的非線性模型外，仍可以使用線性迴歸方法來擬合非線性資料，只不過在此之前，需要對輸入資料進行處理。

多項式迴歸是一種通過增加自變數上的次數，而將資料對映到高維空間的方法，從而提高模型擬合複雜資料的效果。

本文主要運用對比分析方法解釋線性資料、非線性資料、線性模型及非線性模型出發，並深入分析多項式迴歸處理非線性資料的原理、效果及程式碼實現。

在探究多項式迴歸之前，先對線性資料、非線性資料、線性模型及非線性模型做一個詳細的介紹，以便更加深入地理解多項式迴歸在非線性資料集上使用線性模型的奧祕。

一、資料集的線性與非線性

變數之間的線性關係（linear relationship），表示兩個變數之間的關係可以展示為一條直線，即可以使用方程 來擬合。繪製散點圖通常是表示兩個變數之間的線性關係的最簡單的方式。如果散點圖能夠相對均勻地分佈在一條直線的兩端，則說明這兩個變數之間的關係是線性的。而如三角函數（），高次函數（），指數函數（）等等影象不為直線的函數所對應的自變數和因變數之間是非線性關係（non-linear relationship）。

一般情況下，一組資料由多個變數和標籤組成。變數分別與標籤存線上性關係，則稱他們是線性資料。而任意一個變數與標籤之間的需要用三角函數、指數函數等來定義，則稱其為"非線性資料"。

在迴歸中，繪製圖像的是變數與標籤的關係圖，橫座標是特徵，縱座標是標籤，標籤是連續型的，則可以通過是否能夠使用一條直線來擬合影象判斷資料究竟屬於線性還是非線性。

左圖可以用 線性方程來進行擬合，稱為線性資料；而右圖擬合方程為 ， 為非線性方程，因此稱之為非線性資料。

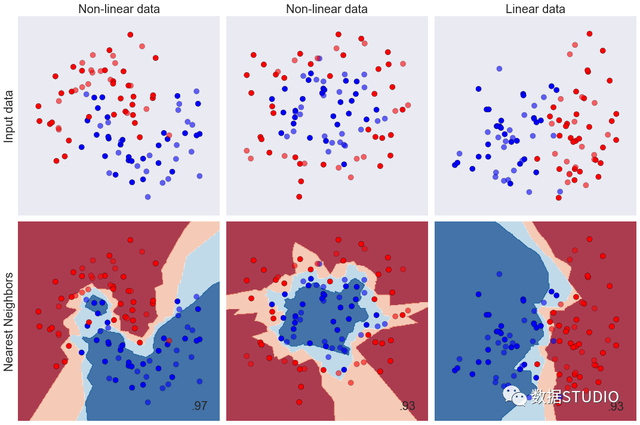
在分類中，繪製的是資料分佈圖，橫縱座標均是資料中的變數，顏色表示標籤資料點。則使用 "是否線性可分" (linearly separable)來劃分分類資料集。當分類資料的分佈上可以使用一條直線來將兩類資料分開時，則資料是線性可分的。反之，資料不是線性可分的。

這些資料與上面資料不同，都不能由一條直線來進行擬合，也沒有均勻分佈在某一條線的周圍，但右圖可以用一條直線將其分開，而左圖卻不能。

二、線性模型與非線性模型

回顧下線性迴歸模型，可以擬合出一組參數向量 ，從而建立一個模型，即線性迴歸模型。其建模過程即尋找參數向量的過程，用於擬合線性資料的線性模型。線性迴歸模型擬合的方程為線性方程，如下

而像決策樹、支援向量機、各類樹的整合模型，以及一切通過三角函數，指數函數等非線性方程來建立的模型。諸如此類的模型並不能像線性迴歸模型一樣，使用形似 的線性方程來擬合數據。但他們被用於擬合非線性資料時，效果出奇的好（甚至過擬合）。

從影象上可以看出，線性迴歸模型無法擬合出這條帶噪音的正弦曲線的真實面貌，只能夠模擬出大概的趨勢，使用線性迴歸模型來擬合非線性資料的效果並不好。這是因為線性模型假定自變數和因變數之間總是存線上性關係。這個假設是很弱的，它僅僅是近似。而非線性的決策樹模型卻通過建立複雜的模型將幾乎每個點都擬合出來了，擬合得太細緻，但相比之下，決策樹在非線性資料上的擬合效果更好一些。

實際中機器學習中的模型很靈活。線性模型可以用來擬合非線性資料，而非線性模型也可以用來擬合線性資料，有的演算法沒有模型也可以處理各類資料，而有的模型可以既可以是線性，也可以是非線性模型。

非線性模型擬合線性資料

非線性模型擬合或處理線性資料的例子非常多，如隨機森林，決策樹等分類演算法在處理線性可分的資料時，其效果並不遜於線性模型等表現。但與此同時，過擬合現象也更加容易出現在非線性模型擬合線性資料上，如利用隨機森林擬合一條直線，因為簡單的一條直線對於非線性模型來說過於簡單，很容易就把訓練集上的訓練得很高，訓練的很低。

非線性模型擬合非線性資料

諸如隨機森林的非線性模型線上性模型上擬合效果不遜於線性模型，但更易過擬合。非線性模型真正的用武之地是非線性資料或非線性可分的資料集，其可以達到線性模型不能逾越的鴻溝。

線性模型擬合非線性資料

線性模型若用來擬合非線性資料或者對非線性可分的資料進行分類，那通常都會表現糟糕。

從上面的圖中，線性模型們的決策邊界都是一條條平行的直線，而非線性模型們的決策邊界是互動的直線、曲線或環形等等。對於分類模型，線性模型的決策邊界是平行的直線，非線性模型的決策邊界是曲線或者交叉的直線。

迴歸模型中，若自變數上的最高次方為1，則模型是線性的

分類模型中，如果一個分類模型的決策邊界上自變數的最高次方為1，則稱這個模型是線性模型。

既是線性也是非線性的模型

有些模型既可以處理線性模型又可以處理非線性模型，如支援向量機。支援向量機的前身是感知機模型，樸實的感知機模型是線性模型，線上性可分資料上表現優秀，但在非線性可分的資料上基本屬於無法使用狀態。

而支援向量機通過選用不同的核函數可以線上性和非線性之間自由切換。如選用線性核函數"linear"，資料沒有進行變換，就是線性模型。當選用非線性核函數時，資料進行升維變化，就是非線性模型。因此支援向量機在對不同的資料集選用合適的核函數，可以較靈活地高效地處理各種類型的資料。

沒有模型的演算法，如KNN，其原理不是建模擬合數據，也沒有線性和非線性模型之分，但能夠直接預測出標籤或做出判斷。

不過這並不代表著我們就完全不能使用線性模型來處理非線性資料了。在現實中，線性模型有著不可替代的優勢----計算速度異常快速，並存在著不得不使用線性迴歸的情況。

三、多項式迴歸

PolynomialFeatures

多項式迴歸通過增加額外的預測項對簡單線性模型進行了拓展，即一個簡單的線性迴歸可以通過從係數構造多項式特徵來擴展。在標準線性迴歸的情況下，對於二維資料，你可能有一個這樣的模型：

如果我們想讓資料擬合一個拋物面而不是一個平面，我們可以把這些特徵合併成二階多項式，使模型看起來像這樣:

更加一般地，多項式函數擬合數據時，多項式定義為

其中 為多項式的階數，即最高次。 是多項式的係數，記做 ，

是關於 非線性函數，但是卻是關於多項式係數 的線性函數。因此可以運用均方誤差對多項式進行評估

狹義線性模型

自變數上不能有高此項，自變數與標籤之間不能存在非線性關係。

廣義線性模型

只要標籤與模型擬合出的參數之間的關係是線性的，模型就是線性的。

線性模型中的升維工具----多項式變化。是一種通過增加自變數上的次數，而將資料對映到高維空間的方法，在sklearn中的類 PolynomialFeatures 設定一個自變數上的次數(大於1)，相應地獲得資料投影在高次方的空間中的結果。

語法

sklearn.preprocessing.PolynomialFeatures (degree=2, interaction_only=False, include_bias=True)

重要參數

degree : integer

多項式中的次數，預設為2

interaction_only : boolean, default = False

布爾值是否只產生互動項，預設為False。就只能將原有的特徵進行組合出新的特徵，而不能直接對原特徵進行升次。

include_bias : boolean

布爾值，是否產出與截距項相乘的 ，預設True

例

>>> from sklearn.preprocessing import PolynomialFeatures>>> import numpy as np>>> X = np.arange(6).reshape(3, 2)>>> Xarray([[0, 1],       [2, 3],       [4, 5]])>>> poly = PolynomialFeatures(degree=2)>>> poly.get_feature_names()['1', 'x0', 'x1', 'x0^2', 'x0 x1', 'x1^2']>>> poly.fit_transform(X)array([[ 1.,  0.,  1.,  0.,  0.,  1.],       [ 1.,  2.,  3.,  4.,  6.,  9.],       [ 1.,  4.,  5., 16., 20., 25.]])>>> # 轉換成DataFrame>>> poly2 = PolynomialFeatures(degree=3)>>> X_2 = poly2.fit_transform(X)>>> pd.DataFrame(data = X_2 ,columns=poly2.get_feature_names())

當我們進行多項式轉換的時候，多項式會產出到最高次數為止的所有低高次項。這個最高次數可以通過 degree=n 來控制。

>>> poly3 = PolynomialFeatures(degree=3, interaction_only=True)>>> X_3= poly3.fit_transform(X)>>> pd.DataFrame(X_3, columns=poly3.get_feature_names())

多項式迴歸處理非線性問題

同樣的一個問題，用線性迴歸模型無法擬合出這條帶噪音的正弦曲線的真實面貌，只能夠模擬出大概的趨勢，而用複雜的決策樹模型又擬合地太過細緻，即過擬合。此時利用多項式將資料升維，並擬合數據，看看結果如何。

程式碼

from sklearn.preprocessing import PolynomialFeatures as PFfrom sklearn.linear_model import LinearRegressionimport numpy as npimport matplotlib.pyplot as pltrnd = np.random.RandomState(42) #設定隨機數種子 X = rnd.uniform(-3, 3, size=100)y = np.sin(X) + rnd.normal(size=len(X)) / 3#將X升維，準備好放入sklearn中 X = X.reshape(-1,1)#多項式擬合，設定高次項d=5#原始特徵矩陣的擬合結果LinearR = LinearRegression().fit(X, y)#進行高此項轉換X_ = PF(degree=d).fit_transform(X)LinearR_ = LinearRegression().fit(X_, y)line = np.linspace(-3, 3, 1000, endpoint=False).reshape(-1, 1) line_ = PF(degree=d).fit_transform(line)#放置畫布fig, ax1 = plt.subplots(1)#將測試資料帶入predict介面，獲得模型的擬合效果並進行繪製ax1.plot(line, LinearR.predict(line), linewidth=2, color='green'         ,label="linear regression")ax1.plot(line, LinearR_.predict(line_), linewidth=2, color='orange',label="Polynomial regression") #將原資料上的擬合繪製在影象上ax1.plot(X[:, 0], y, 'o', c='k')#其他圖形選項ax1.legend(loc="best")ax1.set_ylabel("Regression output") ax1.set_xlabel("Input feature") ax1.set_title("Linear Regression ordinary vs poly") ax1.text(0.8,-1,f"LinearRegression score:n{LinearR.score(X,y)}",fontsize=15)ax1.text(0.8,-1.3,f"LinearRegression score after poly :n{LinearR_.score(X_,y)}",fontsize=15)plt.tight_layout()plt.show()

輸出結果

這裡可以看出，多項式迴歸能夠較好地擬合非線性資料，還不容易發生過擬合，可以說是保留了線性迴歸作為線性模型所帶的"不容易過擬合"和"計算快速"的性質，同時又實現了優秀地擬合非線性資料。

這裡我們使用了 degree=5，在實際應用中，我們並不能一次搞定degree的值。其實，不同的最高次取值，對模型擬合效果有重要的影響。

通過選擇不同的 degree 對資料進行擬合：

程式碼

# 生產資料函數def uniform(size):    x = np.linspace(0,1,size)    return x.reshape(size,1)def create_data(size):    x = uniform(size)    np.random.seed(42) #設定隨機數種子     y = sin_fun(x)+np.random.normal(scale=0.25, size=x.shape)    return x,ydef sin_fun(x):    return np.sin(2*np.pi*x)

X_train,y_train = create_data(20)X_test = uniform(200)y_test = sin_fun(X_test)fig = plt.figure(figsize=(12,8))for i,degree in enumerate([0,1,3,6,9,12]):      plt.subplot(2,2,i+1)    poly = PolynomialFeatures(degree)    X_train_ploy = poly.fit_transform(X_train)    X_test_ploy = poly.fit_transform(X_test)        lr = LinearRegression()    lr.fit(X_train_ploy,y_train)    y_pred = lr.predict(X_test_ploy)    plt.scatter(X_train,y_train,facecolor="none", edgecolor="g", s=25, label="training data")    plt.plot(X_test,y_pred,c="orange",label="fitting")    plt.plot(X_test,y_test,c="k",label="$sin(2pi x)$")    plt.title("N={}".format(order))    plt.legend(loc="best")    plt.ylabel("Regression output") #     plt.xlabel("Input feature")     plt.legend()plt.show()

輸出結果

如圖可見，黃色曲線是預測函數，黑色曲線是無噪聲的原始曲線。

當 degree=0 與 degree=1 時多項式擬合數據效果極差，即欠擬合。其實就是線性模型擬合非線性資料。

當 degree=3、6、9 時，其實已經擬合很好了，當 degree=12 時，多項式函數對噪聲資料有一定的敏感性，即過擬合。

前面有提到使用均方誤差對擬合出的多項式進行評估，擬合數據的目的是最小化誤差函數，因為誤差函數是多項式係數 的二次函數，因此它關於係數 的導數是線性函數，所以誤差函數的最小值有一個唯一解，我們記作 。

程式碼

from sklearn.pipeline import Pipeline # 一種具有最終估計器的轉換管道。文末有介紹from sklearn.metrics import mean_squared_errorimport mathimport seaborn as snsimport matplotlib.patches as mpatches# 資料還是上面例子的資料mse1 = []mse2 = []plt.figure(figsize=(12,6))degrees = [0,1,3,6,9,12]for degree in degrees:    pipe = Pipeline([("poly", PolynomialFeatures(degree=degree)),                     ("lin_reg", LinearRegression())])    pipe.fit(X_train,y_train)    pred1 = pipe.predict(X_train)    train_mse = mean_squared_error(y_train,pred1)        pred2 = pipe.predict(X_test)    test_mse = mean_squared_error(y_test,pred2)           mse1.append(train_mse)    mse2.append(test_mse)# 視覺化sns.pointplot(degrees,mse1,color='orange',label='Train')sns.pointplot(degrees,mse2,color='k',label='Test')orange_patch = mpatches.Patch(color='orange', label='Train MSE')black_patch = mpatches.Patch(color='k', label='Test MSE')plt.legend(handles = [red_patch,blue_patch])plt.show()

輸出結果

由於資料量較少導致模型過擬合，可通過增加資料量，可同時增加模型複雜度（提高冪次degree的值）。但當我們增加冪次的值時，曲線開始高頻震盪。這導致曲線的形狀過於複雜，最終引起過擬合現象。此時可通過增加正則項來約束模型複雜度，即在最小化誤差上增加懲罰項。此處可參見前面章節，嶺迴歸於Lasso迴歸。

此外為了克服多項式迴歸的缺點（為了更好地擬合數據，增加多項式函數的複雜性，特徵數量的增長很難控制），有學者提出使用樣條迴歸法來克服多項式的眾多缺點。這種方法沒有將模型應用到整個資料集中，而是將資料集劃分到多個區間，為每個區間中的資料單獨擬合一個模型。具體可參見[
https://zhuanlan.zhihu.com/p/36535032]

多項式迴歸的原理

由上面可知，用多項式迴歸模型擬合出這條帶噪音的正弦曲線，其原理是泰勒級數展開。

泰勒公式泰勒公式是一個用函數在某點的資訊描述其附近取值的公式。數學家們在柯西中值定理的基礎上，推匯出了泰勒中值定理（泰勒公式）。

若函數 在包含 的某個開區間 上具有 階的導數，那麼對於任一 , 有

一般情況下，泰勒公式在處展開。這樣可以簡化了泰勒公式得到在處的 階泰勒公式，也稱麥克勞林（Maclaurin）公式

由於為與之間的某個值，可令 則其餘項寫為

泰勒公式的幾何意義是利用多項式函數來逼近原函數。

根據泰勒級數展開定理可知，任一函數可以用多項式表示，如

同理， 的泰勒展開為

當線性迴歸的模型太簡單導致欠擬合時，我們就可以通過增加特徵多項式來讓線性迴歸模型更好的擬合數據。

多項式迴歸的可解釋性

線性迴歸是一個具有高解釋性的模型，它能夠對每個特徵擬合出參數以幫助我們理解每個特徵對於標籤的作用。當進行了多項式轉換後，隨著資料維度和多項式次數的上升，方程也變得異常複雜，但多項式迴歸的可解釋性依然是存在的，我們可以使用介面get_feature_names來呼叫生成的新特徵矩陣的各個特徵上的名稱。

案例

加利福利亞房屋資料集

from sklearn.datasets import fetch_california_housing as fchimport pandas as pdhousevalue = fch()X = pd.DataFrame(housevalue.data)y = housevalue.targethousevalue.feature_namesX.columns = ["住戶收入中位數","房屋使用年代中位數","平均房間數目" ,"平均臥室數目","街區人口","平均入住率","街區的緯度","街區的經度"]poly = PolynomialFeatures(degree=2).fit(X,y)poly.get_feature_names(X.columns)X_poly = poly.transform(X) reg = LinearRegression().fit(X_poly,y)coef = reg.coef_[*zip(poly.get_feature_names(X.columns),reg.coef_)]#放到dataframe中進行排序coeff = pd.DataFrame([poly.get_feature_names(X.columns),reg.coef_.tolist()]).T coeff.columns = ["feature","coef"]coeff.sort_values(by="coef").head(10)

輸出結果

四、Pipeline

Scikit-Learn中的Pipeline 將三個模型封裝起來串聯操作，讓模型介面更加簡潔，使用起來方便的減少程式碼量同時讓機器學習的流程變得直觀和更加的優雅。函數 PolynomialRegression()中傳入的超參數degree 是用來指定所得的多項式迴歸中所用多項式的階次。

Pipeline原理示意圖

pipeline最後一步如果有predict()方法我們才可以對 pipeline 使用 fit_predict()，同理，最後一步如果有transform()方法我們才可以對pipeline使用fit_transform()方法。

更多內容請參見
https://scikit-learn.org/stable/modules/generated/sklearn.pipeline.Pipeline.html

X,y = create_data(200) # 利用上面的生產資料函數degree = 6# 利用Pipeline將三個模型封裝起來串聯操作npoly_reg = Pipeline([                    ("poly", PolynomialFeatures(degree=degree)),                    ("std_scaler", StandardScaler()),                    ("lin_reg", LinearRegression())                    ])fig = plt.figure(figsize=(10,6)) poly = PolynomialFeatures(order)poly_reg.fit(X, y)y_pred = poly_reg.predict(X)# 視覺化結果plt.scatter(X,y,facecolor="none", edgecolor="g", s=25, label="training data")plt.plot(X,y_pred,c="orange",label="fitting")# plt.plot(X,y,c="k",label="$sin(2pi x)$")plt.title("degree={}".format(degree))plt.legend(loc="best")plt.ylabel("Regression output") plt.xlabel("Input feature") plt.legend()plt.show()

輸出結果

可以運用如下方法獲取對應模型的介面。

>>> poly_reg.named_steps['lin_reg'].coef_array([[  0.        ,  -0.14987173,  16.4142791 , -65.75198762,         87.4087241 , -45.6444121 ,   7.36587511]])>>> poly_reg.named_steps['poly'].get_feature_names()['1', 'x0', 'x0^2', 'x0^3', 'x0^4', 'x0^5', 'x0^6']