機器之心報道編輯:蛋醬、小舟大神早已遠去,而他的光芒仍在人間。1931 年,奧地利裔美國著名數學家庫爾特 · 哥德爾(Kurt Gdel)在一篇論文《ber formal unentscheidbare Stze der
2021-06-18 19:53:31
機器之心報道
編輯:蛋醬、小舟
大神早已遠去,而他的光芒仍在人間。

1931 年,奧地利裔美國著名數學家庫爾特 · 哥德爾(Kurt Gdel)在一篇論文《ber formal unentscheidbare Stze der Principia Mathematica und verwandter Systeme》中正式發表了不完備性定理。
這一理論使數學基礎研究發生了劃時代的變化,更是現代邏輯史上的重要里程碑。該定理與塔爾斯基的形式語言和真理論,圖靈機和判定問題,一同被讚譽為現代邏輯科學在哲學方面的三大成果。
1951 年,哥德爾獲得愛因斯坦勳章,馮 · 諾依曼評價說:「在現代邏輯中的成就是非凡的、不朽的——他的不朽甚至超過了紀念碑,他是一個里程碑,是永存的紀念碑。」
1978 年,哥德爾在美國普林斯頓市去世,享年 71 歲。死亡報告顯示,哥德爾死於「因人格障礙導致的營養不良」。
今年是哥德爾不完備性定理髮表的 90 週年,為此,Jürgen Schmidhuber 特別發文紀念哥德爾及其卓越的理論貢獻。
「在 2021 年,慶祝哥德爾 1931 年開創性的論文發表 90 週年。這篇論文奠定了理論電腦科學和人工智慧理論的基礎,展示了定理證明、計算、人工智慧、邏輯和數學本身的基礎侷限性,在學術界引起了轟動。這一研究對 20 世紀科學和哲學發展產生了巨大影響。」
庫爾特 · 哥德爾被稱為現代理論電腦科學和人工智慧理論之父,曾被美國《時代週刊》評為 20 世紀最具影響力的 100 位人物之一。

不完備性定理髮表於論文《ber formal unentscheidbare Stze der Principia Mathematica und verwandter Systeme》。
在 1931 年的那項研究中,哥德爾引入了一種通用語言來編碼任意形式化的過程。他使用基於素數因數分解的哥德爾編碼系統。他首先把唯一的自然數指派到在他所處理的算術的形式語言中的每個基本符號。
哥德爾證明了,任何一個形式系統,只要包括了簡單的初等數論描述,而且是自洽的,它必定包含某些系統內所允許的方法既不能證明真也不能證偽的命題。
同時,他證明了演算法定理證明、計算和任何類型的基於計算的 AI 都具有基礎侷限性(有些人誤解了他的結果,認為他證明的是人類優於 AI)。1940 年代至 70 年代的大部分 AI 和定理證明有關,並且都是以哥德爾正規化進行推論的,包括專家系統和邏輯程式設計。
1935 年,阿隆佐 · 丘齊(Alonzo Church)通過證明 Hilbert & Ackermann 著名的 Entscheidungsproblem(判定問題)沒有一般解決方案,推匯出哥德爾結果的推論 / 擴展。丘齊使用了叫做 Untyped Lambda Calculus 的通用編碼語言,這門語言構成了極具影響力的程式語言 LISP 的基礎。
1936 年,阿蘭 · 圖靈引入了另一個通用模型「圖靈機」,至少在計算機領域,它是最著名的模型之一。圖靈重新推導了上述結果。當然,他在 1936 年的論文中同時引用了哥德爾和丘奇。

阿蘭 · 圖靈
同年,Emil Post 發表了另一個獨立的通用計算模型,也引用了哥德爾和 Church 的研究。正是圖靈的工作 (1936) 使哥德爾相信他自己的方法 (1931-34) 和丘齊 (1935) 的方法具備普遍性。
理論電腦科學領域的「哥德爾獎」就是以哥德爾的名字命名的。獎金更高的圖靈獎創建於 1966 年,以表彰那些「對計算機領域具有長久和重大的技術貢獻」。有趣但同時也令人尷尬的是,哥德爾 (1906-1978) 本人從未獲得過一個獎項,且不提他奠定了現代理論電腦科學領域的基礎,而且哥德爾還在他寫給約翰 · 馮 · 諾依曼的著名信件中(1956 年)確定了最著名的開放問題「P= NP?」。
應該提到的是,實際應用中的「人工智慧」比哥德爾對人工智慧基本侷限性的理論分析要古老得多。1914 年,西班牙人 Leonardo Torres y Quevedo 是 20 世紀第一個應用 AI 的先驅,當時他構建了第一個可工作的國際象棋終局棋手。
幾十年後,當人工智慧先驅 Norbert Wiener 在 1951 年巴黎會議上與它對弈時,這臺機器依然給人們留下了深刻的印象,1951 年巴黎會議通常被視為第一個關於人工智慧的會議,儘管 1956 年「人工智慧」這個詞才在達特茅斯(Dartmouth)學會上提出。而在 1951 年,現在被稱為人工智慧的大部分內容仍然被稱為控制論,其重點與現代基於深度神經網路的人工智慧非常一致。
同樣值得一提的是,實用「計算機」科學比哥德爾的理論電腦科學基礎要古老得多。也許世界上第一臺可以實際應用的可程式設計機器是公元 1 世紀製造的自動化劇場。其中可程式設計自動機的能源是一個落錘,拉動纏繞在旋轉圓柱體上的繩子。控制門和木偶的複雜指令序列由複雜的包裝進行編碼。
公元 9 世紀,班努 · 穆薩兄弟發明了一種可以自動演奏樂曲的樂器,它使用旋轉圓柱體上的銷釘儲存控制蒸汽驅動長笛的程式。從本質上說,這正是一臺可以程式設計的機器,並且帶有儲存程式。
大約 1800 年,Joseph-Marie Jacquard 等人在法國建造了第一臺商用程式控制機器,即基於打孔卡的織機,也許他們算是編寫世界上第一個工業軟體的第一批「現代」程式設計師。
這種機器設計思想啟發了 Ada Lovelace 和她的導師 Charles Babbage,當時他們計劃但卻無法構建十進位制的可程式設計通用計算機。1941 年 Zuse 製造出世界上第一臺能程式設計的計算機 Z3,而在 1944 年,Howard Aiken 構建了第一個通用可程式設計機器十進位制的馬克一號(MARK I)。

馬克一號(右面部分)
哥德爾經常被稱為亞里士多德以來最偉大的邏輯學家。《時代》雜誌曾將他列為 20 世紀最有影響力的數學家,儘管一些數學家認為他最重要的研究成果在於邏輯和計算,而不是數學。有些人稱哥德爾的理論是理論電腦科學的基礎,後來理論電腦科學成為一個專門的學科。哥德爾的理論和思想激勵了一代又一代的年輕人學習電腦科學。
在不到一個世紀的時間裡,曾經只存在於偉人腦海中的東西,如今已成為現代社會不可忽視的存在,這些科學家理應獲得更多的鮮花和掌聲。
機器之心報道
編輯:蛋醬、小舟
大神早已遠去,而他的光芒仍在人間。

1931 年,奧地利裔美國著名數學家庫爾特 · 哥德爾(Kurt Gdel)在一篇論文《ber formal unentscheidbare Stze der Principia Mathematica und verwandter Systeme》中正式發表了不完備性定理。
這一理論使數學基礎研究發生了劃時代的變化,更是現代邏輯史上的重要里程碑。該定理與塔爾斯基的形式語言和真理論,圖靈機和判定問題,一同被讚譽為現代邏輯科學在哲學方面的三大成果。
1951 年,哥德爾獲得愛因斯坦勳章,馮 · 諾依曼評價說:「在現代邏輯中的成就是非凡的、不朽的——他的不朽甚至超過了紀念碑,他是一個里程碑,是永存的紀念碑。」
1978 年,哥德爾在美國普林斯頓市去世,享年 71 歲。死亡報告顯示,哥德爾死於「因人格障礙導致的營養不良」。
今年是哥德爾不完備性定理髮表的 90 週年,為此,Jürgen Schmidhuber 特別發文紀念哥德爾及其卓越的理論貢獻。
「在 2021 年,慶祝哥德爾 1931 年開創性的論文發表 90 週年。這篇論文奠定了理論電腦科學和人工智慧理論的基礎,展示了定理證明、計算、人工智慧、邏輯和數學本身的基礎侷限性,在學術界引起了轟動。這一研究對 20 世紀科學和哲學發展產生了巨大影響。」
庫爾特 · 哥德爾被稱為現代理論電腦科學和人工智慧理論之父,曾被美國《時代週刊》評為 20 世紀最具影響力的 100 位人物之一。

不完備性定理髮表於論文《ber formal unentscheidbare Stze der Principia Mathematica und verwandter Systeme》。
在 1931 年的那項研究中,哥德爾引入了一種通用語言來編碼任意形式化的過程。他使用基於素數因數分解的哥德爾編碼系統。他首先把唯一的自然數指派到在他所處理的算術的形式語言中的每個基本符號。
哥德爾證明了,任何一個形式系統,只要包括了簡單的初等數論描述,而且是自洽的,它必定包含某些系統內所允許的方法既不能證明真也不能證偽的命題。
同時,他證明了演算法定理證明、計算和任何類型的基於計算的 AI 都具有基礎侷限性(有些人誤解了他的結果,認為他證明的是人類優於 AI)。1940 年代至 70 年代的大部分 AI 和定理證明有關,並且都是以哥德爾正規化進行推論的,包括專家系統和邏輯程式設計。
1935 年,阿隆佐 · 丘齊(Alonzo Church)通過證明 Hilbert & Ackermann 著名的 Entscheidungsproblem(判定問題)沒有一般解決方案,推匯出哥德爾結果的推論 / 擴展。丘齊使用了叫做 Untyped Lambda Calculus 的通用編碼語言,這門語言構成了極具影響力的程式語言 LISP 的基礎。
1936 年,阿蘭 · 圖靈引入了另一個通用模型「圖靈機」,至少在計算機領域,它是最著名的模型之一。圖靈重新推導了上述結果。當然,他在 1936 年的論文中同時引用了哥德爾和丘奇。

阿蘭 · 圖靈
同年,Emil Post 發表了另一個獨立的通用計算模型,也引用了哥德爾和 Church 的研究。正是圖靈的工作 (1936) 使哥德爾相信他自己的方法 (1931-34) 和丘齊 (1935) 的方法具備普遍性。
理論電腦科學領域的「哥德爾獎」就是以哥德爾的名字命名的。獎金更高的圖靈獎創建於 1966 年,以表彰那些「對計算機領域具有長久和重大的技術貢獻」。有趣但同時也令人尷尬的是,哥德爾 (1906-1978) 本人從未獲得過一個獎項,且不提他奠定了現代理論電腦科學領域的基礎,而且哥德爾還在他寫給約翰 · 馮 · 諾依曼的著名信件中(1956 年)確定了最著名的開放問題「P= NP?」。
應該提到的是,實際應用中的「人工智慧」比哥德爾對人工智慧基本侷限性的理論分析要古老得多。1914 年,西班牙人 Leonardo Torres y Quevedo 是 20 世紀第一個應用 AI 的先驅,當時他構建了第一個可工作的國際象棋終局棋手。
幾十年後,當人工智慧先驅 Norbert Wiener 在 1951 年巴黎會議上與它對弈時,這臺機器依然給人們留下了深刻的印象,1951 年巴黎會議通常被視為第一個關於人工智慧的會議,儘管 1956 年「人工智慧」這個詞才在達特茅斯(Dartmouth)學會上提出。而在 1951 年,現在被稱為人工智慧的大部分內容仍然被稱為控制論,其重點與現代基於深度神經網路的人工智慧非常一致。
同樣值得一提的是,實用「計算機」科學比哥德爾的理論電腦科學基礎要古老得多。也許世界上第一臺可以實際應用的可程式設計機器是公元 1 世紀製造的自動化劇場。其中可程式設計自動機的能源是一個落錘,拉動纏繞在旋轉圓柱體上的繩子。控制門和木偶的複雜指令序列由複雜的包裝進行編碼。
公元 9 世紀,班努 · 穆薩兄弟發明了一種可以自動演奏樂曲的樂器,它使用旋轉圓柱體上的銷釘儲存控制蒸汽驅動長笛的程式。從本質上說,這正是一臺可以程式設計的機器,並且帶有儲存程式。
大約 1800 年,Joseph-Marie Jacquard 等人在法國建造了第一臺商用程式控制機器,即基於打孔卡的織機,也許他們算是編寫世界上第一個工業軟體的第一批「現代」程式設計師。
這種機器設計思想啟發了 Ada Lovelace 和她的導師 Charles Babbage,當時他們計劃但卻無法構建十進位制的可程式設計通用計算機。1941 年 Zuse 製造出世界上第一臺能程式設計的計算機 Z3,而在 1944 年,Howard Aiken 構建了第一個通用可程式設計機器十進位制的馬克一號(MARK I)。

馬克一號(右面部分)
哥德爾經常被稱為亞里士多德以來最偉大的邏輯學家。《時代》雜誌曾將他列為 20 世紀最有影響力的數學家,儘管一些數學家認為他最重要的研究成果在於邏輯和計算,而不是數學。有些人稱哥德爾的理論是理論電腦科學的基礎,後來理論電腦科學成為一個專門的學科。哥德爾的理論和思想激勵了一代又一代的年輕人學習電腦科學。
在不到一個世紀的時間裡,曾經只存在於偉人腦海中的東西,如今已成為現代社會不可忽視的存在,這些科學家理應獲得更多的鮮花和掌聲。
相關文章

機器之心報道編輯:蛋醬、小舟大神早已遠去,而他的光芒仍在人間。1931 年,奧地利裔美國著名數學家庫爾特 · 哥德爾(Kurt Gdel)在一篇論文《ber formal unentscheidbare Stze der
2021-06-18 19:53:31

又一高校出手積體電路領域了!或許是國內對積體電路人才的需求,亦或是國內現在處於高速發展狀態,所以在去年的時候南京就率先成立了晶片大學,緊接著今年清華也成立了積體電路學院
2021-06-18 19:52:21
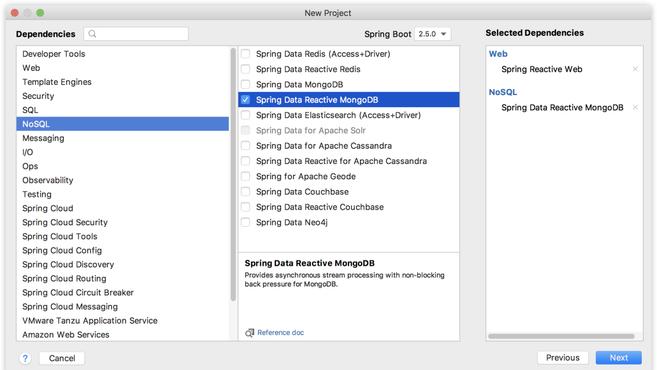
WebFlux 最為人所詬病的是資料庫的支援問題,畢竟資料是一個應用的生命,我們接觸的大部分應用程式都是有資料庫的,而 WebFlux 在這一方面的支援行一直比較弱,這也是大家總是吐槽
2021-06-18 19:33:48

在華為釋出鴻蒙系統之後,一群網友紛紛到小米創始人兼董事長雷軍微博下面催促小米採用鴻蒙系統,然而小米方面婉轉地拒絕了,就在數天後小米宣佈將以MIUI+物聯網系統velaOS走向全
2021-06-18 19:33:31

正如「萬物皆為虛、銷量才為真」這句話所言,想要看該品牌到底如何,看它的銷量就能明白。畢竟,不管廠商們有多麼吹噓自己的產品或者服務,但最後說話的也永遠都是產品的銷量。就拿
2021-06-18 19:33:12

隨著手機的普及率不斷的提高,手機儼然已經成為消費者日常生活中不可或缺的裝置之一,而手機上使用頻率最高的,應當是手機的輸入法。因為無論你是購物還是發訊息,輸入法都是必不可
2021-06-18 19:32:24