1. 為什麼需要散列表?對於線性表和連結串列而言,訪問表中的元素,時間複雜度均為O(n)。即便是通過樹結構儲存資料,時間複雜度也為O(logn)。那麼有沒有一種方式可以將這個時間複
2021-06-28 15:30:05

1. 為什麼需要散列表?
對於線性表和連結串列而言,訪問表中的元素,時間複雜度均為O(n)。即便是通過樹結構儲存資料,時間複雜度也為O(logn)。那麼有沒有一種方式可以將這個時間複雜度降為O(1)呢?當然有,這就是接下來要介紹的散列表。散列表是普通陣列概念的推廣。由於對於普通陣列只要知道其下標位置就可以使用O(1)的時間內訪問任意元素,如果儲存空間允許,我們可以提供一個足夠大的陣列,為每個可能的關鍵字保留一個位置,這個位置也被稱之「槽」,從而可以充分的利用直接定址的技術優勢,其實就是典型的空間換時間。
2. 雜湊函數
既然散列表是對關鍵字進行計算,從而確定該關鍵字對應的資料在儲存中的位置,在下文中統一稱之為「槽」,那麼又該通過什麼方式進行計算呢?其實這個方式就是雜湊函數。雜湊函數的設計對於散列表的效能將起到決定性的作用。因為如果雜湊函數設計不當導致多個關鍵字計算出的結果都是同一個位置,即存在大量的雜湊衝突(也可以稱為雜湊碰撞)。現如今存在的雜湊函數演算法非常多,通常的雜湊演算法都是將關鍵字轉換為自然數,然後通過除法或是乘法進行雜湊。一些簡單的雜湊演算法,比如關鍵字是整數直接使用求餘法;關鍵字是字元串的話,一種可行的演算法是每個字元的ASCII碼相加之後對錶的長度進行取模。對於同一類型的關鍵字的雜湊演算法是多種多樣的,但無論如何應該儘可能的避免雜湊衝突並且保證其雜湊的結果是均勻分佈的。之所以要儘可能的保證雜湊結果是均勻分佈其實也是為了儘可能的避免雜湊衝突。
3.雜湊衝突以及衝突解決
但是無論雜湊演算法設計的多麼完美,雜湊衝突它都是一定存在的。因為對於散列表的大小而言它是固定的,一旦你初始化之後就不會改變。但是對於元素而言是可以無限制地新增的,換句話說就是散列表中的「槽」位,對於關鍵字來說總歸是不夠的,所以就會出現多個關鍵字通過雜湊函數計算出的「槽」位是相同的。
當雜湊衝突出現的時候,主要通過開放定址法、完全雜湊法、分離連結法等其他演算法解決衝突。
1.開放定址法
在開放定址法中,散列表中的每個槽位最多隻會儲存一個元素。當出現雜湊衝突的時候,就會從該槽位出發選擇一個方向(向前或是向後)開始探測,(每次探測的距離為1則稱之為線性探查,距離為某個數字的平方則稱之為平方探查)只要散列表足夠大,總歸是可以找到一個可以儲存的槽位,但是如此花費的時間是相當多的。更糟糕的是,即使散列表相對較空這樣佔據的槽位一旦開始形成,當後面出現本應該放到該槽位的關鍵字由於已被佔據,而不得不進行探測尋找可以儲存的槽位,這種現象也被稱之為聚集。除此之外可以採用雙重雜湊法,使用一組雜湊函數,直到找到空閒的位置為止,一種比較流行的做法是使用兩個相對獨立的雜湊函數hash1(),hash2()。當發生碰撞時,通過步長i進行探測。
(hash1(key) + i * hash2(key)) % TABLE_SIZE
這種雙雜湊如果hash2()設計的不好將會是災難性的。一個好的hash2()表現好的特徵是:1.不會產生0索引、2.可以探測整個散列表
2.分離連結法
在分離連結法中,散列表中出現衝突時,可以通過連結串列的方式將元素連線起來,在對元素進行訪問時,若發現該槽位中是一個連結串列則對該連結串列進行遍歷。此種分離方式並不只是僅限於連結串列,比如一顆樹或是另一個散列表都是可以的。比如即將在下文中提到的HashMap就是使用連結串列+紅黑樹來實現的。
3.再雜湊
如果散列表很多槽位已經被佔據,name操作的運行時間將開始消耗過長,且插入操作可能失敗。此時一種解決方法是建立另外一個大約兩倍大的表,掃描整個原始散列表計算每個元素的新的槽位並將其插入到新的表中,整個操作就被稱為再雜湊。其實本質上就是通過擴容減少衝突。
4.完全雜湊法
雖然全域雜湊和完全雜湊具有良好的理論效能,但實現起來不太方便,前提條件也多。在實際應用上,往往會更偏向其他方式解決衝突。
4.動態擴容
因為散列表在創建的時候其大小是固定的,而關鍵字是不斷被新增到散列表中,所以隨著關鍵字的不斷新增,產生雜湊衝突的概率就會越來越大。因此為了避免雜湊衝突就需要擴大散列表的容量。當已被佔據的「槽」的個數和散列表的大小的比例達到一定的閾值時,就開始執行散列表的擴容,而這個閾值也被稱之為載入因子(或擴容因子)。在擴容的時候,往往需要對原來的關鍵字重新進行雜湊,但是通過某些技巧其實是可以避免再雜湊的情況,比如HashMap的源碼中在擴容的時候就沒有進行再雜湊,這一部分在下文將詳細講解。
5.雜湊在HashMap的應用
1、雜湊函數

在這裡為什麼選擇31作為乘數,為什麼不是偶數或其他奇質數3,5,…,33,37,97…等其他數字? 原因如下:1. 31 是一個奇質數,如果選擇偶數會導致乘積運算時資料溢位,造成資料丟失;2.雜湊碰撞:實驗資料表明乘數為大於等於31的奇質數碰撞概率很小,基本穩定;3.雜湊分佈:實驗資料表明乘數為大於等於31的奇質數雜湊分佈相對來說較為均勻。4.另外在二進位制中,2的5次方是32,那麼也就是 31 * i == (i << 5) -i。這主要是說乘積運算可以使用位移提升效能,同時JVM 也會位移操作的優化。
2、擾動函數

在這裡HashMap並沒有直接將key的雜湊值返回,而是進行了一次干擾計算
(h = key.hashCode()) ^ (h >>> 16)
把雜湊值右移16位,也就是自己長度的一半,之後再與原雜湊值進行異或運算。這樣做的目的就是混合雜湊值中的高位和低位增大隨機性,使得雜湊值分佈更加均勻,減少碰撞。
3、初始化容量

在這裡進行初始化容量的時候,會不斷進行或運算將二進位制數都填上1,目的就是去尋找2的次冪的最小值。如傳入的cap值為9則返回距離9最小的2的次冪值即16。那在這裡為什麼需要尋找2的次冪的最小值呢?
4、插入、連結串列樹化 、紅黑樹




通過源碼分析,HashMap增加元素的過程如下:1. 如果散列表不存在或是其長度為0則進行一次擴容操作2. 通過key的雜湊值對散列表的長度進行與計算獲得槽位2.1 若該槽位對應的元素為空 直接新增一個節點,新增節點後需要判斷是否超過負載閾值,超過則進行擴容。 2.2 該槽位存在值 2.2.1 判斷key是否與當前的key一致 一致時,修改該元素,然後返回舊值。 2.2.2 判斷該槽位對應的元素是否為樹節點,這個樹其實是一顆紅黑樹為樹節點時,則進入putTreeVal()方法,這個方法要做的事簡單地說就是「根據雜湊值遍歷樹的結構,是否可以找到該key,若是可以找到就返回該節點,若是找不到就會新增的一個節點,並且平衡該樹,最終返回一個空值」。putTreeVal()方法在新增節點的是後續返回null最終需要判斷是否超過負載閾值,超過則進行擴容;修改節點時返回該節點資料,則將該樹節點對應的值修改為當前的value並直接返回。 2.2.3 說明這個槽位對應的元素是一個連結串列為連結串列時,則先對連結串列進行遍歷,是否可以找到該key,若可以找到則將該元素,則將該節點的值修改為value並退出;找不到該key時,說明這是一個新增元素,所以會在連結串列的尾部再新增一個節點。新增完節點後還需要判斷該連結串列的長度是否超過了閾值(預設是8),超過閾值後並且表的大小還要超過64,則會將該連結串列進行轉成二叉樹,然後在轉成紅黑樹,在轉換成樹的時候也會記錄各節點的在連結串列中的位置;否則也只會對該散列表進行擴容。最終判斷是否超過負載閾值,超過則進行擴容。
4、負載因子

負載因子是關鍵字與散列表大小的比值,它決定了資料量達到多少之後進行擴容,預設的負載因子為0.75。如果希望以更多的空間換時間,儘量避免雜湊碰撞,則可以手動指定更小的負載因子。
5、擴容元素拆分
當陣列長度不足時,或是當前關鍵字與散列表大小的比值超過了負載因子則進行散列表的擴容。在jdk1.7中,散列表擴容時,需要進行再雜湊的操作,重新計算各個key在新表中的槽位。而在jdk1.8中,擴容機制進行了優化,已經不需要進行再散列了,而是通過該key新的雜湊值與原來的散列表進行與運算【key.hash()&oldCap==0】,如果為0,則不需要修改槽位,否則將該槽位移動到原來的位置+oldCap的位置,即【j+oldCap】。當紅黑樹擴容後的節點數小於 UNTREEIFY_THRESHOLD(預設是6)即小於7個節點數時,紅黑樹則會進行鏈化,因為連結串列在轉成紅黑樹的時候,是有記錄各節點在連結串列中的位置的,所以紅黑樹在轉成連結串列的時候會相對簡單很多。
6、查詢
HashMap查詢元素的過程如下:1. 通過雜湊函數計算並且擾動後的雜湊值 2. 若散列表為空或其大小為0,則直接返回null; 3. 根據計算出的雜湊值與散列表的大小-1做與運算獲得槽位【在表中的下標索引】 4. 該槽位的元素是否為樹節點 4.1 不為樹節點,按連結串列形式進行遍歷 4.2 為樹節點,則按照紅黑樹形式進行遍歷
10、刪除
HashMap刪除元素的過程如下:1. 通過雜湊函數計算並且擾動後的雜湊值 2. 若散列表為空或其大小為0,則直接返回null; 3. 根據計算出的雜湊值與散列表的大小-1做與運算獲得槽位【在表中的下標索引】 4. 該槽位的元素是否為樹節點 4.1 不為樹節點,按連結串列形式進行刪除 4.2 為樹節點,則按照紅黑樹形式進行刪除,刪除之後會進行紅黑樹的平衡
相關文章

1. 為什麼需要散列表?對於線性表和連結串列而言,訪問表中的元素,時間複雜度均為O(n)。即便是通過樹結構儲存資料,時間複雜度也為O(logn)。那麼有沒有一種方式可以將這個時間複
2021-06-28 15:30:05

6月28日下午,小米電視6畫質雙旗艦見面會於線上舉行。小米電視數字系列的全新旗艦——小米電視6至尊版,以及年度真香的畫質輕旗艦——小米電視ES2022款也終於現出了真容。在正
2021-06-28 15:29:31

3Sigma Bootcamp //由五源資本和機器之心聯合主辦的3Sigma Bootcamp將於2021年8月4日至8月8日在上海舉辦。如果你是夢想打破正規化的硬科技領域青年創業者,3Sigma Bootcamp將
2021-06-28 15:29:18
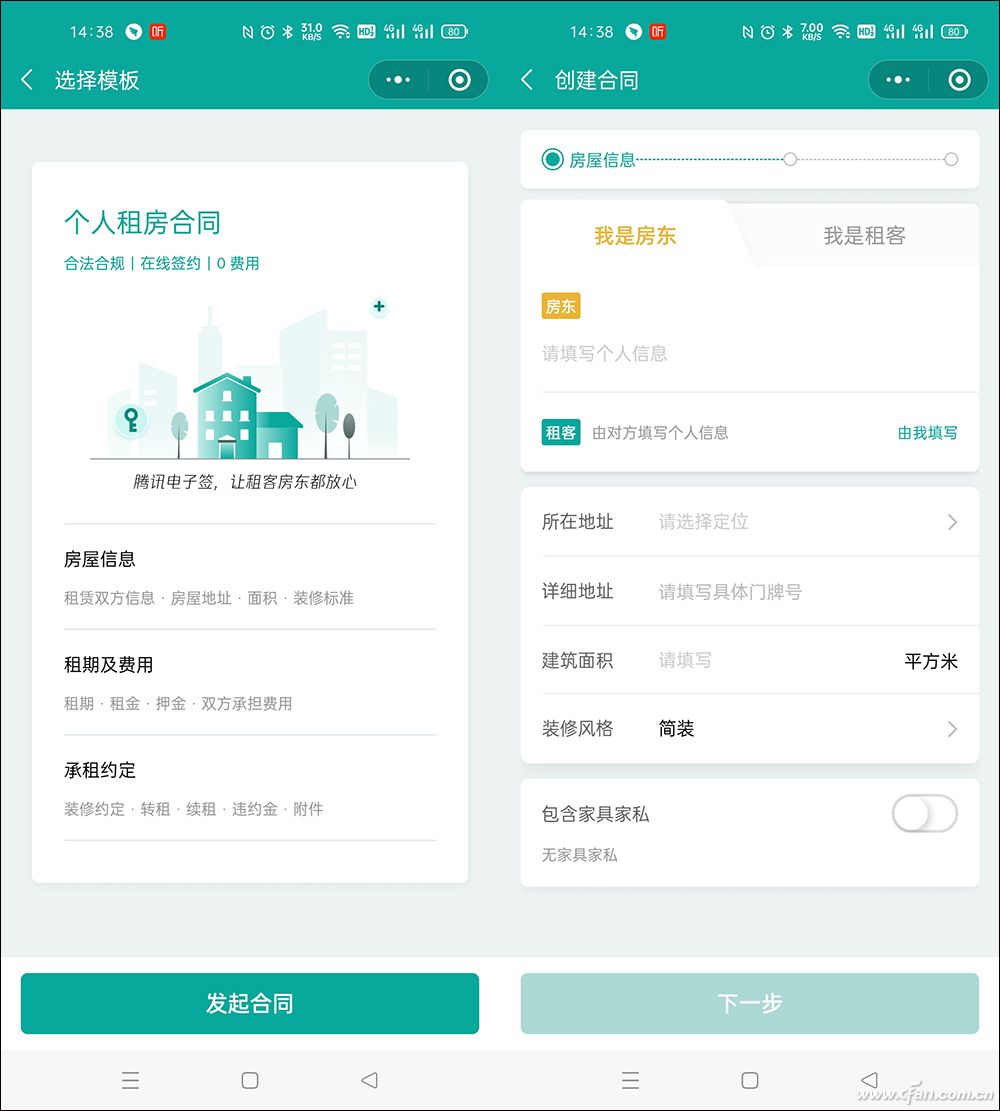
在租房的過程中,房主和租客為了避開中介費,都喜歡繞開中介公司直接簽訂房屋租賃合同。但是,私下籤訂的合同可能不合規,紙質合同也存在丟失損壞風險。當租賃雙方出現合同糾紛又該
2021-06-28 15:28:14

小米電視依靠超值的價格迅速在電視市場站穩腳跟,近年來,小米電視也一直在高階領域進行探索,在此前也曾推出了多款小米電視大師系列產品,並取得了不錯的使用者口碑。今天,小米
2021-06-28 15:10:10

OLED螢幕因為色彩更加鮮豔,對新技術適應性更強,逐漸制霸了手機市場,如今OLED屏手機大行其道,而LCD屏漸漸被大家忽略,價格相對更低、更護眼以及燒屏風險更低,依然存在諸多優勢,不過
2021-06-28 15:09:54