在二叉樹的操作實現中,常常需要對其所有節點進行某種操作,這種對所有節點逐一進行的操作就是遍歷。遍歷二叉樹的遞迴實現遍歷二叉樹是指按照某種順序訪問二叉樹中的每個節點,使
2021-08-23 03:03:37
在二叉樹的操作實現中,常常需要對其所有節點進行某種操作,這種對所有節點逐一進行的操作就是遍歷。
遍歷二叉樹是指按照某種順序訪問二叉樹中的每個節點,使每個節點被訪問一次且僅被訪問一次。其中的訪問可指計算二叉樹中節點的資料資訊,列印該節點的資訊,也包括對節點進行的任何其他操作。
遍歷二叉樹是二叉樹最基本的操作,也是二叉樹其他各種操作的基礎。因為在實際應用中,常常需要按一定順序對二叉樹中的每個節點逐個進行訪問,或查詢節點,然後再進行處理。
二叉樹是非線性資料結構,通過遍歷可使二叉樹中節點由非線性序列得到訪問節點的順序序列。也就是說,遍歷操作使非線性結構線性化。
由二叉樹的定義可知,二叉樹由根節點、根節點的左子樹和根節點的右子樹三部分組成。因此,只要依次遍歷這三部分,就可以遍歷整個二叉樹。
若以D、L、R分別表示訪問根節點、遍歷根節點的左子樹、遍歷根節點的右子樹,則二叉樹的遍歷方式有六種:DLR、LDR、LRD、DRL、RDL和RLD。如果限定先左後右,則只有前三種方式。根據對根的訪問先後順序不同,分別稱DLR為先序(根)遍歷、LDR為中序(根)遍歷和LRD為後序(根)遍歷。
基於二叉樹的遞迴定義,可得遍歷二叉樹的遞迴演算法定義。
1.先序遍歷
若二叉樹為空,則為空操作,否則
(1)訪問根節點;
(2)先序遍歷根節點的左子樹;
(3)先序遍歷根節點的右子樹。
先序遍歷二叉樹的遞迴演算法如下。

2.中序遍歷
若二叉樹為空,則為空操作,否則
(1)中序遍歷根節點的左子樹;
(2)訪問根節點;
(3)中序遍歷根節點的右子樹。
中序遍歷二叉樹的遞迴演算法如下。

3.後序遍歷
若二叉樹為空,則為空操作,否則
(1)後序遍歷根節點的左子樹;
(2)後序遍歷根節點的右子樹;
(3)訪問根節點。
後序遍歷二叉樹的遞迴演算法如下。

4.層次遍歷
所謂二叉樹的層次遍歷,是指從二叉樹的第一層(根節點)開始,從上至下逐層遍歷,在同一層中,則按從左到右的順序對節點逐個訪問。

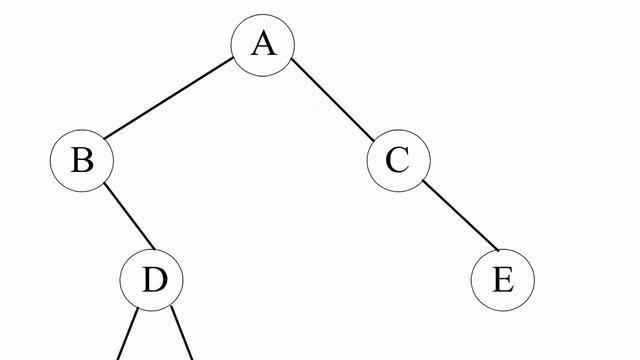
對於如上圖所示的二叉樹,其先序、中序、後序、層次遍歷的序列如下。
先序遍歷:A、B、D、F、G、C、E;
中序遍歷:B、F、D、G、A、C、E;
後序遍歷:F、G、D、B、E、C、A;
層次遍歷:A、B、C、D、E、F、G。
從二叉樹遍歷的定義可知,先序、中序和後序三種遍歷演算法的區別在於訪問根節點和遍歷左、右子樹的先後關係,但都採用了遞迴的方法。而遞迴的實現,一定會採用後進先出的棧。
對於上圖所示的二叉樹,其先序、中序和後序遍歷都是從根節點A開始的,且在遍歷過程中經過節點的路線也是一樣的,只是訪問的時機不同而已。圖6-14所示的從根節點左外側開始到根節點右外側結束的曲線為遍歷二叉樹的路線。沿著該路線按△標記的節點讀得的序列為先序序列,按*標記讀得的序列為中序序列,按#標記讀得的序列為後序序列。

然而,這一路線正是從根節點開始沿左子樹搜尋,當搜尋到最左端,無法再深入下去時,則返回,再逐一進入剛才搜尋時遇到節點的右子樹,再進行如此的搜尋和返回,直到最後從根節點的右子樹返回到根節點為止。先序遍歷是在搜尋時遇到節點就訪問,中序遍歷是在從左子樹返回時遇到節點訪問,後序遍歷是在從右子樹返回時遇到節點訪問。
在這一過程中,返回節點的順序與搜尋節點的順序相反,正好符合棧結構後進先出的特點,因此,可以利用棧將遞迴演算法改寫成非遞迴演算法。
在沿左子樹搜尋時,深入一個節點入棧一個節點,若為先序遍歷,則在入棧之前訪問它;當沿左分支深入不下去時,則返回,即從棧中彈出前面壓入的節點;若為中序遍歷,則此時訪問該節點,然後從該節點的右子樹繼續深入;若為後序遍歷,則將此節點再次入棧,然後從該節點的右子樹繼續深入,深入一個節點入棧一個節點,深入不下去時再返回,直到第二次從棧裡彈出該節點,即從右子樹返回時,才訪問之。
1.先序遍歷的非遞迴實現
在下面演算法中,二叉樹以二叉連結串列存放,一維陣列stack[MAXSIZE]用以實現棧,變數top用來表示當前棧頂的位置。


2.中序遍歷的非遞迴實現
中序遍歷的非遞迴演算法實現,只需將先序遍歷的非遞迴演算法中的printf(p->data)移到p=stack[top]和p=p->rchild之間即可。


3.後序遍歷的非遞迴實現
後序遍歷非遞迴演算法比較複雜。由於後序遍歷要求左、右子樹都訪問完後,最後訪問根節點。說明節點在第一次出棧後,還需再次入棧。也就是說,節點要入兩次棧,出兩次棧,而訪問節點是在第二次出棧時訪問。因此,為了區別同一個節點指針的兩次出棧,設定一標誌flag,當節點指針進、出棧時,其標誌flag也同時進、出棧。

後序遍歷二叉樹的非遞迴演算法如下。
在演算法中,一維陣列stack[MAXSIZE]用於實現棧的結構,指針變數p指向當前要處理的節點,top為棧頂指針,用來表示當前棧頂的位置。


無論是遞迴還是非遞迴遍歷二叉樹,由於每個節點僅被訪問一次,則不論按哪一種次序進行遍歷,對含n個節點的二叉樹,其時間複雜度均為O(n)。所需輔助空間為遍歷過程中棧的最大容量,即樹的深度,最壞情況下為n,即空間複雜度也為O(n)。
作者:有出路
連結:https://juejin.cn/post/6996949323707580447
來源:掘金
相關文章
在二叉樹的操作實現中,常常需要對其所有節點進行某種操作,這種對所有節點逐一進行的操作就是遍歷。遍歷二叉樹的遞迴實現遍歷二叉樹是指按照某種順序訪問二叉樹中的每個節點,使
2021-08-23 03:03:37
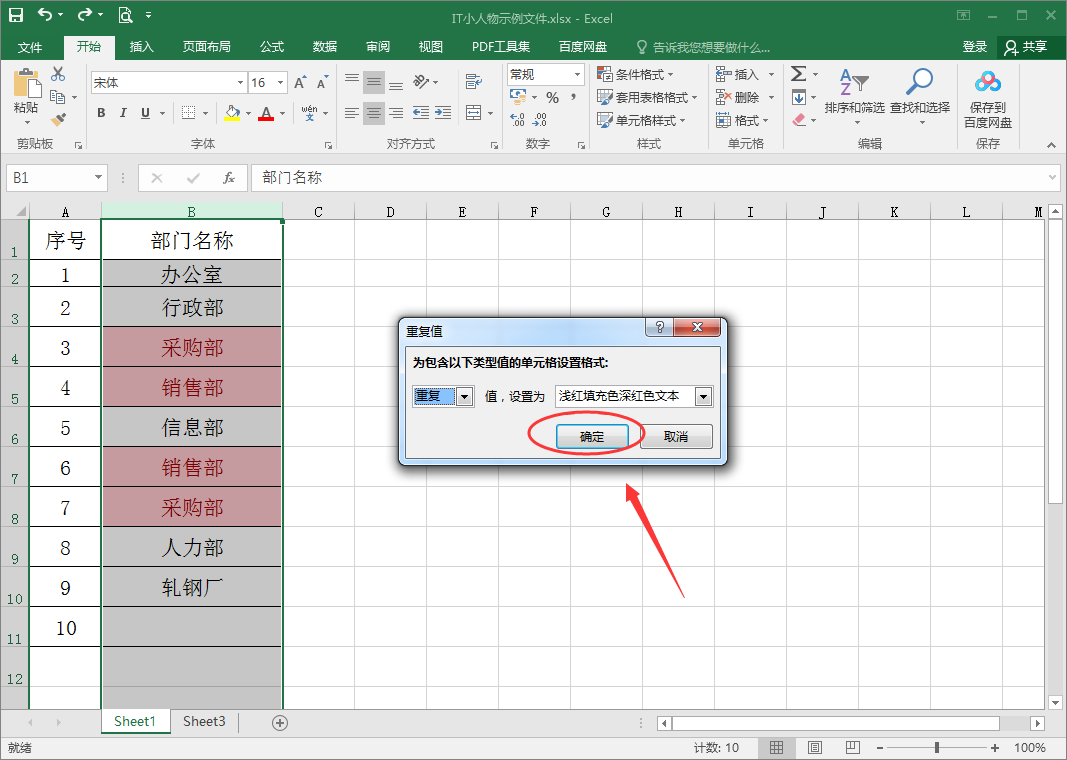
在日常辦公中經常會使用excel表格,在表格中有一些重複的資料,有時需要將它們篩選出來,那麼怎麼快速篩選這些重複的資料呢?1、以如下表格為例,介紹下如何篩選出表格中重複的資料;2
2021-08-23 03:03:30

近年來,眼看中國晶片領域迅速發展,感受到威脅的有關方面不斷加大對中國半導體產業的封鎖力度,導致部分中國科技公司蒙受了不同程度的損失。不過,在打壓力度越來越大的同時,中國半
2021-08-23 03:03:17

眾所周知,今年華為釋出的旗艦手機P50已經成為了一款4G手機,而在釋出會上,餘承東說,我們的5G晶片也只能當4G用,原因就是5G射頻晶片華為也買不到了。短時間來看,華為已經不可能推出5
2021-08-23 03:03:09

最近一段時間,關於蘋果新品的訊息大量出現。就現有的訊息而言,即將到來的蘋果新品包括iPhone 13系列手機、iPad系列平板電腦、Apple Watch系列智慧手錶、AirPods系列耳機以及M
2021-08-23 03:02:55
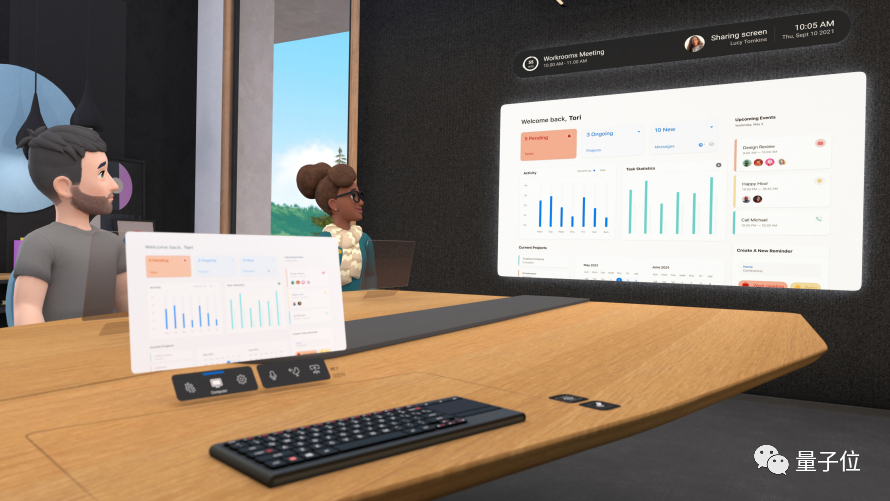
用自己的真實化身和同事們一起線上開會,是一種怎樣的體驗?圖片新冠疫情的爆發讓很多人打工人都體驗到了遠端辦公這一新工作方式。但它最大的缺點就是與同事之間的交流很侷限。
2021-08-23 03:02:30