<em>Mac</em>Book项目 2009年学校开始实施<em>Mac</em>Book项目,所有师生配备一本<em>Mac</em>Book,并同步更新了校园无线网络。学校每周进行电脑技术更新,每月发送技术支持资料,极大改变了教学及学习方式。因此2011
2021-06-01 09:32:01
原文連結:Histogram of Oriented Gradients
(文中的圖片均來自翻譯原文)
特徵描述子一張圖片或者一個圖片塊的一種表示,通過提取有用資訊並扔掉多餘的資訊來簡化影象。
通常,特徵描述子將一張大小為width×height×3 (通道數)的圖片化成一個長度為n的特徵向量/陣列。以HOG特徵為例,輸入影象的大小是64×128×3,輸出是一個長度為3780的特徵向量。
注意一點,HOG特徵也可以是其它大小,但這裡我使用原文獻中使用的大小,這樣你可以更容易地通過一個具體的例子來理解這個概念。
上面這些聽起來不錯,但是對於一張圖片的資訊,哪些是有用的哪些是冗餘的呢?為了定義這個有用資訊,我們需要知道它對什麼有用。顯然,特徵向量對於我們看一張影象沒什麼用。但是,它對影象識別和目標檢測這樣的任務很有用。將由這些演演算法生成的特徵向量作為支援向量機等分類演演算法的輸入往往可以得到不錯的結果。
但是,對於分類任務來說,哪類特徵是有用的呢?讓我們先用一個例子討論一下。假設我們想設計一個目標檢測器來檢測襯衫或者外套上的鈕釦。通常鈕釦是圓的(可能在圖片上會是橢圓)而且一般會有一些孔用於縫紉。你可以在一張鈕釦的圖片上執行邊緣檢測,僅僅通過觀察邊緣影象就可以判斷它是不是一個鈕釦。在這個例子中,邊緣資訊是有用的而顏色資訊是無用的。此外,特徵也需要有區分能力。例如,從某一張圖片中提取的一個好的特徵應具備區分鈕釦和其他圓心物體(如硬幣和車輪)的能力。
對於HOG特徵描述子,選用梯度方向的分佈作為特徵。一張影象的梯度(x和y方向的導數)很有用因為在邊緣和拐角(強度變化劇烈的區域)處的梯度幅值很大。而且我們知道邊緣和拐角比其他平坦的區域包含更多關於物體形狀的資訊。
在這一節,我們將詳細介紹HOG描述子的計算。為了解釋計算的每個步驟,我們使用一個圖片塊進行分析。
正像之前提到的那樣,HOG特徵通過在一張64×128的圖片塊上計算得到以用於行人檢測。當然完整的圖片可以是任意的尺寸。通常我們會在圖片的不同位置分析多尺度圖片塊。唯一的要求就是圖片塊需要有固定的長寬比。在我們的例子中,圖片塊需要保持1:2 的縱橫比。比如:100×200, 128×256或者1000×2000都可以,但101×205就不滿足要求。
為了解釋這一點,我在下面選用了一張720×475的圖片。我們在圖上選擇一個圖片塊來計算HOG特徵。這個小塊是從原影象上裁剪下來的並且縱橫比調整為64×128。這樣我們就準備好計算這個圖片塊的HOG特徵了。

原始文獻中Dalal和Triggs也將 γ γ 矯正放在預處理步驟中,但是帶來的增益很小因此這裡我們忽略這一步。
為了計算HOG特徵,我們需要先計算影象水平和豎直方向的梯度。畢竟我們想要計算梯度直方圖。這一步可以很容易通過的核對對原影象進行濾波實現。

我們也可以使用OpenCV中的Sobel運算元(kernel size設為1)得到相同的結果。
// C++ gradient calculation.
// Read image
Mat img = imread("bolt.png");
img.convertTo(img, CV_32F, 1/255.0);
// Calculate gradients gx, gy
Mat gx, gy;
Sobel(img, gx, CV_32F, 1, 0, 1);
Sobel(img, gy, CV_32F, 0, 1, 1);
# Python gradient calculation
# Read image
im = cv2.imread('bolt.png')
im = np.float32(im) / 255.0
# Calculate gradient
gx = cv2.Sobel(img, cv2.CV_32F, 1, 0, ksize=1)
gy = cv2.Sobel(img, cv2.CV_32F, 0, 1, ksize=1)下一步我們可以用下面的公式來計算梯度的幅值和方向。

如果你使用OpenCV,可以通過下面的cartToPolar函數實現。
// C++ Calculate gradient magnitude and direction (in degrees) Mat mag, angle; cartToPolar(gx, gy, mag, angle, 1);
在Python中實現如下:
# Python Calculate gradient magnitude and direction ( in degrees ) mag, angle = cv2.cartToPolar(gx, gy, angleInDegrees=True)
下圖顯示了計算得到的梯度:

左:X方向梯度幅值圖;中:Y方向梯度幅值圖;右:梯度幅值圖
X方向的梯度凸顯豎直的線而Y方向的梯度凸顯水平的線。梯度的幅值出現在強度變化劇烈的地方。在強度平坦的區域幾乎沒有梯度。我故意忽略了梯度方向圖,因為在影象上顯示梯度方向沒有傳遞太多的資訊。
梯度影象移除了很多不必要的資訊(比如不變的背景),突出了輪廓資訊。也就是說,你僅僅通過看梯度影象還是可以辨認出影象有有一個人。
對於每一個畫素,梯度都會有幅值和方向。對於彩色影象,需要分別計算3個通道的梯度(如上圖所示)。而該畫素點的幅值是這3個通道梯度幅值的最大值,方向是最大梯度幅值對應的角度。
在這一步,影象被分成8×8的很多cell,而梯度直方圖是在這些cell中計算出來的。

我們一會兒將學習直方圖,但在那之前,我們先理解一下為什麼將影象切分成很多8×8的cell。使用特徵描述子來描述影象中的一小塊的一個重要原因是它用更為緊湊的表示方法刻畫了原影象。一個8×8的圖片塊包含了8×8×3=192個畫素值。而這個影象塊的每個畫素點梯度資訊包含梯度幅值和方向兩個值,一共是8×8×2=128個值,這128個值可以通過用包含9個bin的直方圖表示成一個一維陣列(包含9個值)。這樣做不僅可以使影象表示更緊湊,而且在一個圖片塊中計算直方圖可以讓這種表示方法對噪聲有更強的魯棒性。單個畫素的梯度資訊可能包含噪聲,而一個8×8的圖片塊中的直方圖讓這種表示方法對噪聲更不敏感。
但是為什麼要用8×8的圖片塊呢?為什麼不是32×32?這是由我們需要尋找的特徵比例決定的。HOG特徵起初是被用來檢測行人的。8×8的cell在一張64×128的行人圖片塊中的足以捕捉感興趣的特徵(如人臉、頭頂等)。
上述梯度直方圖本質上是一個包含9個數位的向量(或陣列),這9個數位分別對應0°、20°、40°、… 160°。
我們來看一下圖片塊中的一個8×8 cell的梯度是什麼樣子。

中:一個RGB cell及其梯度(用箭頭表示);右:cell中的梯度大小和方向(數位表示)
如果你是一個計算機視覺領域新手,中間的這幅圖為你提供了很多資訊。它展示了用箭頭表示的梯度資訊的梯度圖——箭頭的指向表示了梯度的方向而箭頭的長度表示了梯度的大小。需要注意到的一點是箭頭的方向指向了影象強度變化的方向,而梯度大小表示了強度的變化有多大。
在右邊的圖上,我們發現8×8的cell中表示梯度的數位有一點細微的差別——角度實在0°到180°之間的而不是0°到360°之間。這些叫做“無符號梯度”,因為因為一個正負方向的兩個梯度由同一個數位表示。換句話說,某一個梯度箭頭和它對應的另一個值(加上180°對應的那個值)被當作是同一個梯度。根據經驗,無符號梯度被證明比有符號梯度效果更好。一些HOG特徵的實現程式碼會允許你選擇是否使用有符號梯度。
下一步就是在這些8×8的cells上建立梯度直方圖。直方圖包含9個bins分別對應著0°、20°、40°、… 160°。
下圖解釋了具體的過程。我們在和上面那個圖一樣的8×8的cells上檢視梯度的大小和方向。每個bin是基於梯度方向選出來的,對應的票數(加在當前bin上的值)對應著梯度的大小。我們先來看看用藍色圓圈出來的畫素,它的梯度的角度是80°,大小為2。因此它在第5個bin上加2。下圖中用紅色圈出來的梯度的角度是10°,大小是4。由於10°是在0°和20°的中間位置, 因此改位置梯度對應票數被一分為二加到相鄰的兩個bin上。

還有一個細節需要注意。如果梯度方向大於160°。此時梯度的角度位於160°和180°之間。我們知道0°和180°是一樣的(無符號梯度),因此在下面的例子中,梯度方向為165°的畫素按比例將梯度大小分配到0°和160°的bin中。

8×8的cell中所有畫素處的梯度按照方向將梯度大小累加到9個bin以建立最後的梯度直方圖。上圖中的cell對應的梯度直方圖如下:

在我們的表示結果中,y軸對應0°。你可以發現上面的直方圖中有大量的權重(梯度大小的投票結果)在0°和180°附近,這從另外一個角度說明了在這個cell中大部分梯度方向要麼朝上要麼朝下。

在上述步驟中,我們基於影象的梯度建立直方圖。一張圖片的梯度對整體的光線的光線比較敏感。如果你把影象所有的畫素值除以2使整張影象變暗,梯度的大小也會變為原來的一半,從而梯度直方圖的值也會將為原來的一半。理想情況下,我們想讓特徵描述子獨立於光線變化。換句話說,我們想要“標準化”這個直方圖使它不受光線變化的影響。
在我講梯度直方圖如何標準化之前,我們先來看看一個長度為3的向量如何標準化。
假設我們有一個RGB顏色向量[128, 64, 32]。這個向量的長度是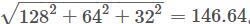
。這也叫做向量的L2範數。將這個向量的所有元素除以向量長度146.64就可以得到一個標準化的向量[0.87, 0.43, 0.22],現在考慮另外一個向量,這個向量的元素是第一個向量的兩倍即2×[128, 64, 32]=[256, 128, 64]。你可以自己計算一下它對應的標準化結果,發現結果仍然是[0.87, 0.43, 0.22],這個值和第一個RGB向量的標準化向量相同。你可以發現標準化一個向量移除了這個向量的尺度資訊。
現在我們知道如何標準化一個向量,你可能想到當計算HOG特徵的時候你可以像之前標準化一個3×1向量一樣去標準化9×1的直方圖。這的確是個不錯的想法,但是更好的做法是標準化一個更大的16×16的block。一個16×16的block包含4個直方圖,這4個直方圖可以連線成一個36×1的向量,而且這個向量仍然可以像那個3×1的向量一樣進行標準化。每次標準化後,整個視窗移動8個畫素並再次計算得到一個36×1的標準化向量,就這樣一直重複這個過程。
為了計算整個圖片塊最終的特徵向量所有的36×1的向量被連線成一個大向量。這個大向量的維度是多少大呢?
我們來計算:
- 1. 我們有多少個不同位置的16×16的block?一共有 (64-8)/8=7 個水平的位置和 (128-8)/8=15 個豎直的位置,所以總計7×15=105個。
- 2. 每一個16×16的block被表示成一個36×1的向量。因此,當我們把他們連線成一個大向量的時候會得到一個36×105=3780維度的向量。
一個影象塊梯度特徵的視覺化通常通過在所有8×8的cell裡畫出對應的標準化的9×1向量(直方圖)。如下圖所示。你會注意到直方圖的主要方向捕捉了人的形狀,尤其是在軀幹和腿附近。
不幸的是,目前在OpenCV中並沒有一個簡單的方法方法來視覺化HOG特徵。
到此這篇關於Python與C++中梯度方向直方圖的實現的文章就介紹到這了,更多相關Python 梯度方向直方圖內容請搜尋it145.com以前的文章或繼續瀏覽下面的相關文章希望大家以後多多支援it145.com!
相關文章

<em>Mac</em>Book项目 2009年学校开始实施<em>Mac</em>Book项目,所有师生配备一本<em>Mac</em>Book,并同步更新了校园无线网络。学校每周进行电脑技术更新,每月发送技术支持资料,极大改变了教学及学习方式。因此2011
2021-06-01 09:32:01

综合看Anker超能充系列的性价比很高,并且与不仅和iPhone12/苹果<em>Mac</em>Book很配,而且适合多设备充电需求的日常使用或差旅场景,不管是安卓还是Switch同样也能用得上它,希望这次分享能给准备购入充电器的小伙伴们有所
2021-06-01 09:31:42

除了L4WUDU与吴亦凡已经多次共事,成为了明面上的厂牌成员,吴亦凡还曾带领20XXCLUB全队参加2020年的一场音乐节,这也是20XXCLUB首次全员合照,王嗣尧Turbo、陈彦希Regi、<em>Mac</em> Ova Seas、林渝植等人全部出场。然而让
2021-06-01 09:31:34

目前应用IPFS的机构:1 谷歌<em>浏览器</em>支持IPFS分布式协议 2 万维网 (历史档案博物馆)数据库 3 火狐<em>浏览器</em>支持 IPFS分布式协议 4 EOS 等数字货币数据存储 5 美国国会图书馆,历史资料永久保存在 IPFS 6 加
2021-06-01 09:31:24

开拓者的车机是兼容苹果和<em>安卓</em>,虽然我不怎么用,但确实兼顾了我家人的很多需求:副驾的门板还配有解锁开关,有的时候老婆开车,下车的时候偶尔会忘记解锁,我在副驾驶可以自己开门:第二排设计很好,不仅配置了一个很大的
2021-06-01 09:30:48

不仅是<em>安卓</em>手机,苹果手机的降价力度也是前所未有了,iPhone12也“跳水价”了,发布价是6799元,如今已经跌至5308元,降价幅度超过1400元,最新定价确认了。iPhone12是苹果首款5G手机,同时也是全球首款5nm芯片的智能机,它
2021-06-01 09:30:45