「實戰案例」基於Python語言開發的信用評分卡

今天，給各位資料粉帶來的是參加過CDA 認證level II 課程培訓的學員比較熟悉的一個經典資料探勘應用案例——金融常見信用評分卡的開發解析。

基於Python語言開發信用評分卡

Part 1 學會信用評分卡，我都能幹什麼？

01、信用評分卡的應用場景

與信用評分卡掛鉤的信用評級在全球金融領域有廣泛應用。它涉及到公司管理，企業債發行，企業融資，企業上市，企業併購，個人炒股和購買公司債券等多個場景。

企業債發行
企業主體信用評級越高，意味著該企業抗風險能力、盈利能力越強，發債融資成本越低。作為企業董事會，管理者，決策者應該瞭解企業主要財務指標，瞭解自身企業評級。
企業發債時都需要評級。國內評級這塊主要分為AAA、AA+、AA、AA-、A+。企業評級過低會限制某些工具的發行額度、交易場所可質押性等等
如果是評級太低，企業發行債券沒人買。目前廣大投資者的投資門檻是AA。
企業上市
企業上市融資時也需要信用評級。目前國內只有優質企業才能上市融資，上市牌照是很難拿的。如果財務指標和資質不達標，則不能上市。
企業併購
企業併購是企業之間的兼併和收購行為。如果收購方不能很好了解對方企業評級，買來的企業可能是包裝過的垃圾企業。失敗企業併購會讓企業背上巨大債務負擔。
個人炒股
個人炒股投資者如果不懂企業評級，也難以買到優質股，容易被人忽悠買到垃圾股。建議不會資料科學的人趁早離開股市和金融投資，否則可能欠下鉅額債務。
如果個人通過學習機器學習模型，可以識別有價值企業，股票，債券，財富升值概率顯著高於不懂模型的人。

本案我們主要聚焦的是【金融信貸】場景中的信用評分卡開發實施全過程。

如果你是急性子，那麼可以在我們小程式中提前看全案

02、金融信貸基礎概念

在進行項目實施開發前，對應用場景進行深入瞭解，是我們資料人的基本功。

信用風險

信貸業務，又稱貸款業務，是商業銀行等信貸機構最重要的資產業務和主要贏利手段。信貸機構通過放款收回本金和利息，扣除成本後獲得利潤。對有貸款需求的使用者，信貸機構首先要對其未來的還款表現進行預測，然後將本金借貸給還款概率大的使用者。但這種借貸關係，可能發生信貸機構（通常是銀行）無法收回所欠本金和利息而導致現金流中斷和回款成本增加的可能性風險，這就是信用風險，它是金融風險的主要類型。

信用評分

在信貸管理領域，關於客戶信用風險的預測，目前使用最普遍的工具為信用評分卡，它源於20世紀的銀行與信用卡中心。在最開始的審批過程中，使用者的信用等級由銀行聘用的專家進行主觀評判。而隨著資料分析工具的發展、量化手段的進步，各大銀行機構逐漸使用統計模型將專家的評判標準轉化為評分卡模型。如今，風險量化手段早已不侷限於銀行等傳統借貸機構，持牌網際網路公司的金融部門、持牌消費金融公司等均有成體系的風險量化手段。其應用的範圍包括進件、貸後管理及催收等。信用評分不但可以篩選高風險客戶，減少損失發生，也可以找出相對優質的客戶群，發掘潛在商機。

顧名思義，評分卡是一張有分數刻度和相應閾值的表。對於任何一個使用者，總能根據其資訊找到對應的分數。將不同類別的分數進行彙總，就可以得到使用者的總分數。信用評分卡，即專門用來評估使用者信用的一張刻度表，這裡我們舉一個簡單的例子：假設我們有一個評分卡，包含四個變數（特徵），即居住條件、年齡、貸款目的和現址居住時長（見表2-1）

用表2-1這張簡單的評分卡，我們能輕而易舉地計算得分。一個47歲、租房、在當前住址住了10年、想借錢度假的申請者得到53分（20+17+16+0=53），另一個25歲、有自己的房產、在當前住址住了2年、想借錢買二手車的人也同樣得到53分（5+30+9+9=53）。同樣地，一個38歲、與父母同住、在當前住址住了18個月、想借錢裝修的人也得到53分（15+20+4+14=53）。事實上，我們一共有七個組合可以得到53分，他們雖然各自情況都不一樣，但對貸款機構來說代表了同樣的風險水平。該評分系統採用了補償機制，即借款人的缺點可以用優點去彌補。

總的來說，信用評分卡就是通過用資料對客戶還款能力和還款意願進行定量評估的系統。從20世紀發展至今，其種類已非常多，目前應用最廣泛最多的主要分為以下四種：

• 申請評分卡（ApplicationCard）：申請評分卡通常用於貸前客戶的進件審批。在沒有歷史平臺表現的客群中，外部徵信資料及使用者的資產質量資料通常是影響客戶申請評分的主要因素。

• 行為評分卡（BehaviorCard）：行為評分卡用於貸中客戶的升降額度管理，主要目的是預測客戶的動態風險。由於客戶在平臺上已有歷史資料，通常客戶在該平臺的歷史表現對行為評分卡的影響最大。

• 催收評分卡（CollectionCard）：催收評分卡一般用於貸後管理，主要使用催收記錄作為資料進行建模。通過催收評分對使用者制定不同的貸後管理策略，從而實現催收人員的合理配置。

• 反欺詐評分卡（Anti-fraudCard）：反欺詐評分卡通常用於貸前新客戶可能存在的欺詐行為的預測管理，適用於個人和機構融資主體。

其中前三種就是我們俗稱的「ABC」卡。A卡一般可做貸款0-1年的信用分析；B卡則是在申請人一定行為後，有了較大消費行為資料後的分析，一般為3-5年；C卡則對資料要求更大，需加入催收後客戶反應等屬性資料。

四種評分卡中，最重要的就是申請評分卡，目的是把風險控制在貸前的狀態；也就是減少交易對手未能履行約定契約中的義務而造成經濟損失的風險。違約風險包括了個人違約、公司違約、主權違約，本案例只講個人違約。

案例背景

發放貸款給合適的客戶是銀行收入的一大來源，在條件允許的範圍內，銀行希望貸出去的錢越多越好，貸款多意味著對應的收入也多，但是如果把錢貸給了信用不好的人或者企業，就會面臨貸款收不回來的情況。

對於貸款申請的審批，傳統人工審批除了受審批人員的專業度影響外，也會受到其主觀影響，另一方面專業人員的培養通常也需要一個較長的週期。 而信用評分卡技術的變數、評分標準和權重都是給定的。同一筆業務，只要錄入要素相同，就會給出一個參考結果。既提高了審批效率也減少了人為因素的干擾，如人工審批過程中的隨意性和不一致性。確保了貸款審批標準的客觀性、標準化和一致性；保證風險特徵相近的貸款申請能夠得到相似的審批結果，如審批通過與否、授信額度、利率水平等。

信用評分卡技術在20世紀50年代即廣泛應用於消費信貸，尤其是在信用卡領域。隨著資訊科技的發展和資料的豐富，信用評分卡技術也被用於對小微企業貸款的評估，最初是擁有大量客戶資料資訊的大型銀行。如富國銀行1993年首先在小微企業貸款領域應用信用評分卡技術。隨後，美國很多社群銀行等中小銀行也開始廣泛應用小微企業信用評分系統。

現中國的某銀行信用卡中心的貸款申請業務近期又增長了10%，原來的申請評分卡已出現數據偏移，監測到審批准確度有下降趨勢。作為信用卡中心的風控建模分析師，小王接到風控總監下發的任務：基於近兩年的歷史資料（見「資料集介紹」的Train_data.csv），重新建立一張「申請評分卡」用於預測申請者未來是否會發生90天以上的逾期行為，以此來判斷給哪些客戶予以發放，哪些客戶予以拒絕。

資料集介紹

• 訓練資料：Train_data.csv。該資料即有特徵X又有標籤y，是小王用來建模的資料。

• 預測資料：Predict_data.csv。該資料只有特徵X沒有標籤y，為小王需要預測的資料。也即新進的申請信用卡的客戶相關資訊。

基於Python語言開發信用評分卡

Part 2 信用評分卡如何做資料準備工作

匯入相關依賴模組

# 載入所需包
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import os
import woe.feature_process as fp
import woe.eval as eval
from collections import Counter
from sklearn.model_selection import train_test_split
import seaborn as sns

plt.rc('font', family='SimHei', size=13) # 顯示中文
plt.rcParams['axes.unicode_minus'] = False # 用來正常顯示負

import sys
sys.path.append('E:大資料實驗室_教研部案例集自定義函數') # 新增自定義函數檔案所在的環境路徑
from summary_df import data_summary #用於資料探查
from score_scale import score_scale
from score_predict import score_predict

資料探索

os.chdir(r"E:大資料實驗室_教研部案例集案例1_信用評分卡data")
data_org = pd.read_csv("Train_data.csv")

data_summary(data_org)

資料準備

資料清洗-ALL資料

data_org.drop_duplicates(inplace=True)

#data_org.shape
#(149391, 11)

• 可見資料中存在重複行。

a = Counter(data_org['Label'])
print("原資料集的正負樣本量為：",a)
print("原資料集好壞樣本的比例為：{:.5f}".format(a[0]/a[1]))

原資料集的正負樣本量為： Counter({0: 139382, 1: 10009})
原資料集好壞樣本的比例為：13.92567

• result: 我們知道一般建模所需的好壞客戶樣本比率約為3:1～5:1。評分卡建模通常要求正負樣本的數量都不少於1500個。但樣本量也並非越大越好，當總樣本量超過50000個時，模型的效果將不再隨著樣本量的增加而有顯著變化了，而且資料處理與模型訓練過程也較為耗時。

• 這裡我們需要對樣本做欠取樣（Subsampling）:

• 負樣本取10000條

• 正樣本取40000條

資料篩選與資料平衡

from sklearn.utils import shuffle
data_org = shuffle(data_org) # 全體資料做隨機打亂
data_bad = data_org[data_org['Label']==1] # 壞客戶
data_good = data_org[data_org['Label']==0] # 好客戶
data_bad_select = data_bad.iloc[:10000,:] #選前10000條壞客戶
data_good_select = data_good.iloc[:40000,:] #選前40000條好客戶
data_select = pd.concat([data_bad_select,data_good_select]) #最終資料

# data_select.shape
#(50000, 11)

拆分訓練集和測試集

from sklearn.model_selection import train_test_split
from collections import Counter
# 資料提取與資料分割
X = data_select.drop(['Label'],axis=1) # 特徵列
y = data_select['Label'] # 標籤列
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3,random_state=0)
print("訓練集正負樣本資料量：{}".format(Counter(y_train)))
print("測試集正負樣本資料量：{}".format(Counter(y_test)))

訓練集正負樣本資料量：Counter({0: 28017, 1: 6983})
測試集正負樣本資料量：Counter({0: 11983, 1: 3017})

資料清洗-訓練資料

缺失值處理

檢視缺失值分佈情況

import missingno as msno # 處理缺失值的包,需要安裝

msno.matrix(X_train)
plt.show()

plt.gray()

缺失值處理方法的選擇,主要依據是業務邏輯和缺失值佔比,在對預測結果的影響儘可能小的情況下,對缺失值進行處理以滿足演算法需求,所以要理解每個缺失值處理方法帶來的影響,下面的缺失值處理方法沒有特殊說明均是對特徵(列)的處理:

1. 佔比較多:如80%以上,直接刪除該變數

• 如果某些行缺失值佔比較多,或者缺失值所在欄位是苛刻的必須有值的,刪除行

1. 佔比一般:如30%-80%:將缺失值作為單獨的一個分類

• 如果特徵是連續的,則其他已有值分箱

• 如果特徵是分類的,考慮其他分類是否需要重分箱

1. 佔比少:10%-30%:多重插補:認為若干特徵之間有相關性,則可以相互預測缺失值

• 需滿足的假設:MAR:Missing At Random:資料缺失的概率僅和已觀測的資料相關,即缺失的概率與未知的資料無關,即與變數的具體數值無關

• 迭代(迴圈)次數可能的話超過40,選擇所有的變數甚至額外的輔助變數

• 詳細的計算過程參考:Multiple Imputation by Chained Equations: What is it and how does it work?

1. 佔比較少:10%以下，單一值替換,如中位數,眾數，或者從業務理解上用0值、特殊值填充

2. 在決策樹中可以將缺失值處理融合到演算法裡:按比重分配

這裡的佔比並不是固定的,例如缺失值佔比只有5%,仍可以用第二種方法,主要依據業務邏輯和演算法需求

本資料的缺失值處理邏輯:

• 對於信用評分卡來說,由於所有變數都需要分箱,故這裡缺失值作為單獨的箱子即可

• 對於最後一列Dependents,缺失值佔比只有2.56%,作為單獨的箱子資訊不夠,故做單一值填補,這列表示家庭人口數,有右偏的傾向,且屬於計數的資料,故使用中位數填補

• 這裡沒必要進行多重插補,下面的多重插補只是為了讓讀者熟悉此操作

單一值替換填充缺失值

# Dependents的缺失值用其中位數替換
NOD_median = X_train["Dependents"].median()
X_train["Dependents"].fillna(NOD_median,inplace=True) # fillna填補缺失值的函數,這裡用中位數填補
X_train["Dependents"].fillna(NOD_median,inplace=True) # 對測試集填充缺失值
#MonthlyIncome 列的缺失值超過5%，可作為單獨的一個分類處理。這裡統一將賦值為-8
X_train["MonthlyIncome"].fillna(-8,inplace=True)
X_train["MonthlyIncome"].fillna(-8,inplace=True)

C:Anaconda3libsite-packagespandascoregeneric.py:6287: SettingWithCopyWarning:
A value is trying to be set on a copy of a slice from a DataFrame
See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy
self._update_inplace(new_data)

check資料是否還有缺失值

a = data_summary(X_train)
data_missing_summary = a[a['percent']<1]
if
data_missing_summary.shape[0]==0:
print('資料已經沒有缺失值！')
else:
print('資料還存在缺失值，請輸出資料框data_missing_summary檢視缺失情況！')

資料已經沒有缺失值！

異常值處理

異常值處理的常用方法:

1. 刪除對應的樣本資料，即所在的行

2. 替換成缺失值,當缺失值處理

3. 蓋帽法處理

結合業務邏輯和演算法需求判斷是否需要處理異常值以及如何處理,一般情況下蓋帽法即可,即將極端異常的值改成不那麼異常的極值。不過一些演算法例如決策樹中連續變數的異常值也可以不做處理。

自定義蓋帽法函數

蓋帽法將某連續變數均值上下三倍標準差範圍外的記錄替換為均值上下三倍標準差值，即蓋帽處理。

def cap(x,lower=True,upper=True):
"""
函數功能：蓋帽法處理異常值。
參數解釋：
x： 表示輸入的Series物件
lower：表示是否替換1%分位數
upper：表示是否替換99%分位數
"""
# 生成分位數:1%和99%的分位數
quantile = [0.01,0.99]
Q01,Q99=x.quantile(quantile).values.tolist()
#替換異常值為指定的分位數
if lower:
out = x.mask(x<Q01,Q01)
if upper:
out = x.mask(x>Q99,Q99)
return(x)

# 先保留原資料X_train蓋帽法中的極端值，以備後面訓練集和預測集處理其異常值時使用
df_min_max = X_train.apply(lambda x:x.quantile([0.01,0.99]))

#蓋帽法處理異常值
X_train = X_train.apply(cap)

data_summary(X_train)

資料清洗-測試集資料

# 用訓練的資訊填充
X_test["Dependents"].fillna(NOD_median,inplace=True) # 對測試集填充缺失值
X_test["MonthlyIncome"].fillna(-8,inplace=True)

def cap2(x,df_min_max,lower=True,upper=True):
"""
函數功能：用訓練集中的蓋帽法極端值處理測試集的異常值。
參數解釋：
x： 表示輸入的Series物件；
df_min_max：是訓練集中的蓋帽法極端值資料框。
"""
col_name = x.name
Q01,Q99 = df_min_max[col_name].values
#替換異常值為指定的分位數
if lower:
out = x.mask(x<Q01,Q01)
if upper:
out = x.mask(x>Q99,Q99)
return(x)

# 用訓練集中的蓋帽法極端值處理測試集的異常值
for itr in df_min_max.columns:
X_test[itr] = cap2(X_test[itr],df_min_max)

# 合併資料X,Y
data_train = pd.concat([X_train,y_train],axis=1)
data_test = pd.concat([X_test,y_test],axis=1)

訓練資料特徵處理

WOE分箱

我們要製作評分卡，最終想要得到的結果是要給各個特徵進分檔，以便業務員能夠根據新客戶填寫的資訊為客戶打分。我們知道變數（即特徵）的形態可分為離散型和連續型，離散型天然就是分檔的，因此，我們需要重點如何使連續變數分檔，即連續變數離散化。

連續變數離散化，我們也常稱為分箱或者分組操作。它是評分卡製作過程中個非常重要的步驟，是評分卡最難，也是最核的思路。目的就是使擁有不同屬性的客戶被分成不同的類別，進而評上不同的分數。在評分卡建模流程中，我們常用WOE（Weight of Evidence，跡象權數）方法對變數進行分箱。

WOE分箱的好處：

• 避免變數值中出現極端值（Outliers）的情形，

• 減少模型過度配適（Overfitting）的現象。

Python程式碼實現woe

"""
woe分箱, iv and transform:
woe包的使用條件：因變數y的列名必須為"target",列值必須為0或1.
"""
data_train.rename(columns={'Label': 'target'}, inplace=True) # 修改列名為"target"
civ_dict ={}
all_cnt = len(data_train) # 所有樣本資料量
n_positive = sum(data_train['target']) # 正樣本資料量
n_negtive = all_cnt - n_positive # 負樣本資料量
for column in set(data_train.columns)-set(["target"]):
if data_train[column].dtypes == 'object':
civ = fp.proc_woe_discrete(data_train, column, n_positive, n_negtive, 0.05*all_cnt, alpha=0.02)
else:
civ = fp.proc_woe_continuous(data_train, column, n_positive, n_negtive, 0.05*all_cnt, alpha=0.02)
civ_dict[column]=civ

--------------process continuous variable:Age---------------
-----------process continuous variable:Dependents-----------
-------process continuous variable:OverDue_60_89days--------
---------process continuous variable:OverDue_90days---------
----------process continuous variable:CreditLoans-----------
-----------process continuous variable:DebtRatio------------
-------process continuous variable:OverDue_30_59days--------
---------process continuous variable:MortgageLoans----------
-----process continuous variable:AvailableBalanceRatio------
---------process continuous variable:MonthlyIncome----------

變數的IV值

用與之相關的另一個重要概念，IV值（Information Value，資訊值）則用來衡量該變數（特徵）對好壞客戶的預測能力。

檢視每個變數對應的IV值

civ_df = eval.eval_feature_detail(list(civ_dict.values()),out_path='
output_feature_detail_20210218.csv') # 輸出分箱結果
# 整理輸出每個變數的IV值
iv_result_a = civ_df[['var_name','iv']].drop_duplicates()
iv_result = iv_result_a['iv']
iv_result.index = iv_result_a['var_name'].values

Age
Dependents
OverDue_60_89days
OverDue_90days
CreditLoans
DebtRatio
OverDue_30_59days
MortgageLoans
AvailableBalanceRatio
MonthlyIncome

# 檢視每個變數的IV值
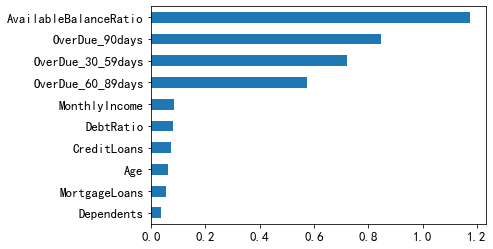
iv_result.sort_values().plot(kind="barh")

AvailableBalanceRatio 1.173317
OverDue_90days 0.845325
OverDue_30_59days 0.723239
OverDue_60_89days 0.574336
MonthlyIncome 0.084926
DebtRatio 0.082108
CreditLoans 0.073128
Age 0.063129
MortgageLoans 0.054396
Dependents 0.035709
Name: iv, dtype: float64

• 可見所有的IV值均大於0.02,故這裡使用所有變數

# 刪除iv值過小的變數
iv_thre = 0.02 #閾值設定為0.02
keep_vars_iv = iv_result[iv_result > iv_thre]# 篩選出iv值（大於閾值）有辨別能力的變數

keep_vars_iv

Age 0.063129
Dependents 0.035709
OverDue_60_89days 0.574336
OverDue_90days 0.845325
CreditLoans 0.073128
DebtRatio 0.082108
OverDue_30_59days 0.723239
MortgageLoans 0.054396
AvailableBalanceRatio 1.173317
MonthlyIncome 0.084926
Name: iv, dtype: float64

相關係數熱力圖

通過變數直接的相關性係數，建立相關性矩陣，觀察變數之間的關係，可以進行初步的多重共線性篩選。

全部變數的相關資訊熱力圖

p_corr = data_train.corr() # 相關係數矩陣，對稱矩陣
p_corr_tril = np.tril(p_corr,0) # 因此取下三角矩陣
label_col = p_corr.columns
res= pd.DataFrame(p_corr_tril,columns=label_col,index=label_col)
sns.heatmap(res,cmap='Blues');

部分變數相關度（>threshold）熱力圖

#只相關係數較高的值，比如大於threshold以上的值
threshold = 0.75 # 閾值，通常取0.75,0.8附近的值
p_corr_tril[p_corr_tril<=threshold]=0.01 # 相關度小於threshold的值都置為0.01

label_col = p_corr.columns
res2= pd.DataFrame(p_corr_tril,columns=label_col,index=label_col)
sns.heatmap(res2,cmap='Blues');

col=['OverDue_30_59days','OverDue_60_89days', 'OverDue_90days']
keep_vars_iv.loc[col]

OverDue_30_59days 0.723239
OverDue_60_89days 0.574336
OverDue_90days 0.845325
Name: iv, dtype: float64

• 可以卡看出'OverDue3059days','OverDue6089days', 'OverDue90days'這三個變數之間具有非常高的相關度。為剔除多重共線性的影響，我們這裡只保留IV值最大的變數'OverDue90days'，刪除'OverDue3059days','OverDue6089days'。

# 經過IV值和相關度篩選後保留的變數
keep_vars = set(keep_vars_iv.index) - {'OverDue_30_59days','OverDue_60_89days'}

訓練集和測試集WOE特徵轉換

keep_var_woe={} # 篩選後保留的變數{變數名：變數名_woe}
for i in keep_vars:
keep_var_woe[i] = i+'_woe'

#WOE特徵轉換
for var_name,var_woe in keep_var_woe.items():
data_train[var_woe] = fp.woe_trans(data_train[var_name], civ_dict[var_name])
data_test[var_woe] = fp.woe_trans(data_test[var_name], civ_dict[var_name])

X_train_woe = data_train[keep_var_woe.values()] # train集的WOE特徵
X_test_woe = data_test[keep_var_woe.values()] # test集的WOE特徵

print("訓練集經過WOE轉換後的shape：{}".format(X_train_woe.shape))
print("測試集經過WOE轉換後的shape：{}".format(X_test_woe.shape))

訓練集經過WOE轉換後的shape：(35000, 8)
測試集經過WOE轉換後的shape：(15000, 8)

基於Python語言開發信用評分卡

Part3 信用評分卡模型構建

邏輯迴歸建模

網格調參

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GridSearchCV

cv_params ={ 'C': np.arange(0.1,1,0.1),
'penalty': ['l1', 'l2', 'elasticnet', 'none'],
'solver': ['newton-cg', 'lbfgs', 'liblinear', 'sag', 'saga']
}
model = LogisticRegression()
gs = GridSearchCV(estimator=model,
param_grid=cv_params,
scoring='roc_auc',
cv=5,
verbose=1,
n_jobs=4)
gs.fit(X_train_woe,y_train)
print('測試集得分:{0}'.format(gs.score(X_test_woe,y_test)))
# print('每輪迭代運行結果:{0}'.format(grid_search.scorer_))
print('參數的最佳取值:{0}'.format(gs.best_params_))
print('最佳模型得分:{0}'.format(gs.best_score_))

Fitting 5 folds for each of 180 candidates, totalling 900 fits
測試集得分:0.8223083325618374
參數的最佳取值:{'C': 0.4, 'penalty': 'l2', 'solver': 'liblinear'}
最佳模型得分:0.8295380458229852

建模

from sklearn.linear_model import LogisticRegression
other_params = {'C': 0.4, 'penalty': 'l2', 'solver': 'liblinear'}
LR_model = LogisticRegression(**other_params)
LR_model.fit(X_train_woe, y_train)
print("變數名：n",list(keep_var_woe.keys()))
print("各個變數係數：n",LR_model.coef_)
print("常數項：n",LR_model.intercept_)

變數名：
['Age', 'Dependents', 'CreditLoans', 'DebtRatio', 'OverDue_90days', 'MortgageLoans', 'AvailableBalanceRatio', 'MonthlyIncome']
各個變數係數：
[[ 0.32460639 0.60488285 -0.25729929 0.84472115 0.73975662 0.54027275
0.7871042 0.16668148]]
常數項：
[-1.37892239]

模型評估

模型的評價指標一般有Gini係數、K-S值和AUC值，基本上都是基於評分卡分數的。但是從理論上評分分數是依據預測為正樣本的概率計算而得，因此基於這個概率計算的指標也是成立的。
下面我們用sklearn庫中的函數計算模型的AUC值和K-S值，以此初步判斷模型的優劣。

from sklearn.metrics import confusion_matrix,roc_auc_score,roc_curve, auc,precision_recall_curve
y_pred_train = LR_model.predict(X_train_woe)
y_pred_test = LR_model.predict(X_test_woe)

訓練集的混淆矩陣：
[[27141 876]
[ 4657 2326]]
測試集的混淆矩陣：
[[11598 385]
[ 2032 985]]

# 預測的分值
y_score_train = LR_model.predict_proba(X_train_woe)[:,1] # 通過 LR_model.classes_ 檢視哪列是label=1的值
y_score_test = LR_model.predict_proba(X_test_woe)[:,1]
# 分別計算訓練集和測試集的fpr,tpr,thresholds
train_index = roc_curve(y_train, y_score_train) #計算fpr,tpr,thresholds
test_index = roc_curve(y_test, y_score_test) #計算fpr,tpr,thresholds

AUC值

ROC曲線是以在所有可能的截斷點分數下，計算出來的對評分模型的誤授率（誤授率表示模型將違約客戶誤評為好客戶，進行授信業務的比率）和1-誤拒率（誤拒率表示模型將正常客戶誤評為壞客戶，拒絕其授信業務的比率）的數量所繪製而成的，AUC值為ROC曲線下方的總面積

# AUC值
roc_auc_train = roc_auc_score(y_train, y_score_train)
roc_auc_test = roc_auc_score(y_test, y_score_test)
print('訓練集的AUC:', roc_auc_train)
print('測試集的AUC:', roc_auc_test)

訓練集的AUC: 0.8297773383440796
測試集的AUC: 0.8223083325618374

• 訓練集和測試集的AUC值相差不大，沒有發生過擬合的情況

我們再繪製訓練集的ROC曲線與測試集的ROC曲線

KS曲線

K-S 測試圖用來評估評分卡在哪個評分區間能夠將正常客戶與違約客戶分開。根據各評分分數下好壞客戶的累計佔比，就可完成K-S測試圖。

print("訓練集的KS值為：{}".format(max(train_index[1]-train_index[0])))
print("測試集的KS值為：{}".format(max(test_index[1]-test_index[0])))

訓練集的KS值為：0.5117269204064546
測試集的KS值為：0.5067980932328976

# ------------------------- KS 曲線
---------------------------
繪製訓練集與測試集的KS曲線

需要注意的是實際業務中資料需要這樣準備：模型開發前，我們一般會將資料分為：訓練集train、測試集test、跨時間資料OOT（train和test是同一時間段資料，一般三七分，oot是不同時間段的資料，用來驗證模型是否適用未來場景）通過這樣的技術保證模型最終可靠穩定。

生成評分卡

評分卡輸出

# 用自定義的評分卡函數score_scale生成評分卡，參數可見具體的函數
r=score_scale(LR_model,X_train_woe,civ_df,pdo=20,score=600,odds=10)
# 輸出最終的評分卡
r.ScoreCard.to_excel("ScoreCard.xlsx",index=False)
print("評分卡最大值和最小值區間為：{}".format(r.minmaxscore))

評分卡最大值和最小值區間為：[447, 640]

基於評分的KS值

繪製結果如下：

策略建議

由訓練集的KS值可知，570分是好壞樣本的最佳分隔點。測試集對其進行驗證，KS值為569,基本一致。因此我們可在訓練集的KS值上下10分內可做如下策略：

• 580分以上的直接予以通過；

• 560分以上的直接予以拒絕；

• [560,580]之間的人群，可以加入人工判斷進行稽核。

以上只是我們給出的策略建議，實際問題和需求遠比這裡複雜，風控人員可以根據具體業務需求給出更加貼合實際業務的策略建議。

新資料的預測

資料準備

# 讀取預測資料
data_predict = pd.read_csv("Predict_data.csv")
# 缺失值的處理
data_predict["Dependents"].fillna(NOD_median,inplace=True) #用訓練集填資訊充缺失值
data_predict["MonthlyIncome"].fillna(-8,inplace=True)
# 異常值的處理：用訓練集中的蓋帽法極端值處理預測集的異常值
for itr in df_min_max.columns:
data_predict[itr] = cap2(data_predict[itr],df_min_max)
# WOE特徵轉換
for var_name,var_woe in keep_var_woe.items():
data_predict[var_woe] = fp.woe_trans(data_predict[var_name], civ_dict[var_name])
X_predict_woe = data_predict[keep_var_woe.values()] # train集的WOE特徵
print("用於預測的資料集經過WOE轉換後的shape：{}".format(X_predict_woe.shape))

用於預測的資料集經過WOE轉換後的shape：(101503, 8)

預測

# 預測客戶的評分結果
score_result = score_predict(data_predict,r)
# 預測為正樣本的概率
X_predict_woe = data_predict[keep_var_woe.values()]
# 合併評分和概率
y_score_predict = LR_model.predict_proba(X_predict_woe)[:,1] # 通過 LR_model.classes_ 檢視哪列是label=1的值
y_score_predict = pd.Series(y_score_predict).to_frame(name='預測為違約客戶的概率')

# 保留使用者ID、預測評分和預測概率三列資訊，並輸出
data_predict_score = score_result[['UserID','Score']].rename(columns={'Score':'預測評分'})
predict_result = pd.concat([data_predict_score,y_score_predict],axis=1)
# 生成「策略建議」策列
cut_off = 570 #切分值
f = 10 #上下浮動值
fuc = lambda x:'通過' if x>cut_off+f else '拒絕' if x<cut_off-f else '人工介入稽核'
predict_result['策略建議'] = predict_result['預測評分'].map(fuc)
predict_result.to_excel("predict_result.xlsx",index=False)# 輸出預測結果to excel

predict_result.head(20) #檢視前20行

結束語

至此，我們已經用python實現了一個申請評分卡的開發過程，並在結尾給出了策略建議。資料化後的風控極大提高了銀行的審批效率，這是傳統的人工稽核不可比擬的，也正是大資料時代帶給我們的便利。

另外需要注意的是，在實際中，模型上線還需要持續追蹤模型的表現，一般是每個月月初給全量客戶打分，並生成前端和後端監控報告。由於篇幅的原因，在此不做詳述，有興趣的讀者可做相關查閱。